Least Squares

Mes11/6/21About 4 min

Least Squares

最小絕對偏差法 Least absolute deviation

假設現在給你這些點

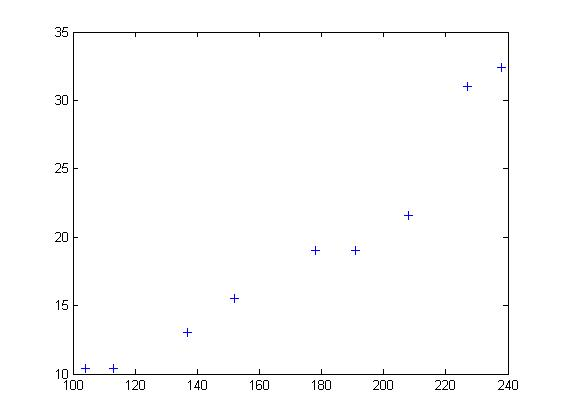
(圖源：wiki)

我們沒辦法用一條直線來通過這些全部的點，但我們可以像這樣找到誤差最小的直線：

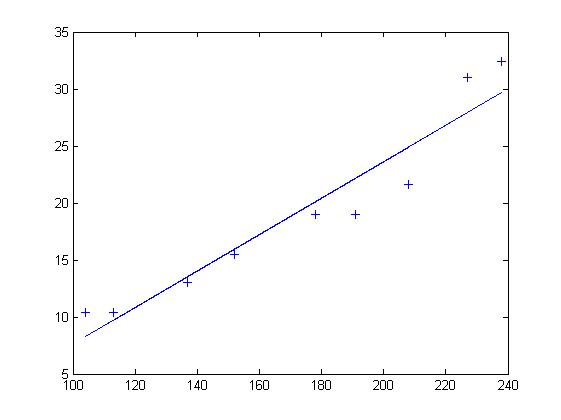
(圖源：wiki )

這條直線可以幫助我們預測資料的方向

假設 $a_{1} x_{i} + a_{0}$ 是這條直線上的第 i 個值， $y_{i}$ 是第 i 個給定的 y 值(原本的 y 值)，我們期望誤差最小，所以我們想要找到 $a_{0}$ 、 $a_{1}$ 最小化這個式子：

$E_{\infty} (a_{0}, a_{1}) = m a x_{1 \leq i \leq 10} {| y_{i} - (a_{1} x_{i} + a_{0}) |}$

這個方法稱作 minimax approach，我們還可以換個方法，找絕對偏差的最小值：

$E_{1} (a_{0}, a_{1}) = Σ_{i = 1}^{10} | y_{i} - (a_{1} x_{i} + a_{0}) |$

那我們要找最小值，也就是說我們要找到 $a_{0}$ 、 $a_{1}$ 符合下面這兩條式子：

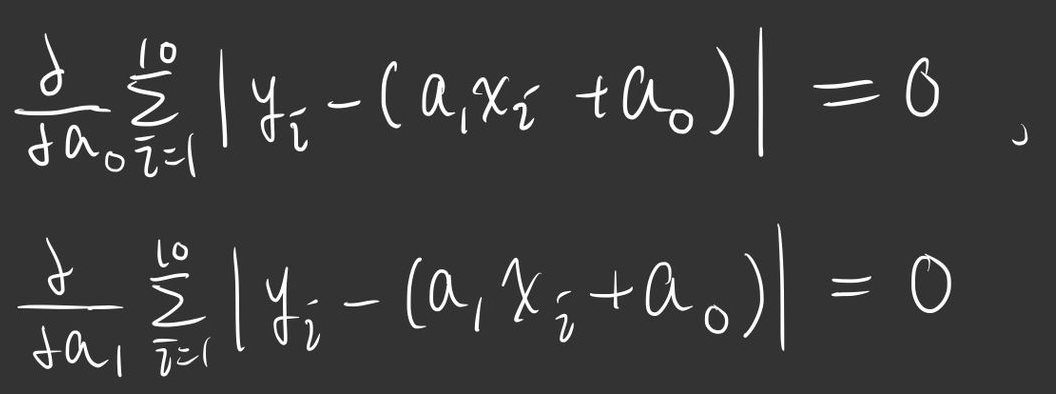
這個方法叫做最小絕對偏差法(least absolute deviation)，但問題是這兩條有絕對值，微分的處理很麻煩，所以下一個方法就出來了

最小平方法 Least Square

剛剛是因為絕對值微分很麻煩，所以這邊就把誤差平方：

$E_{2} (a_{0}, a_{1}) = Σ_{i = 1}^{10} [y_{i} - (a_{1} x_{i} + a_{0})]^{2}$

這樣的話就解決了微分的問題，這樣一來不但微分好算，而且還是 convex 可以找到最佳解

正規方程式 Normal Equations

我們繼續找最小值，對上方的 $E_{2}$ 做偏微：

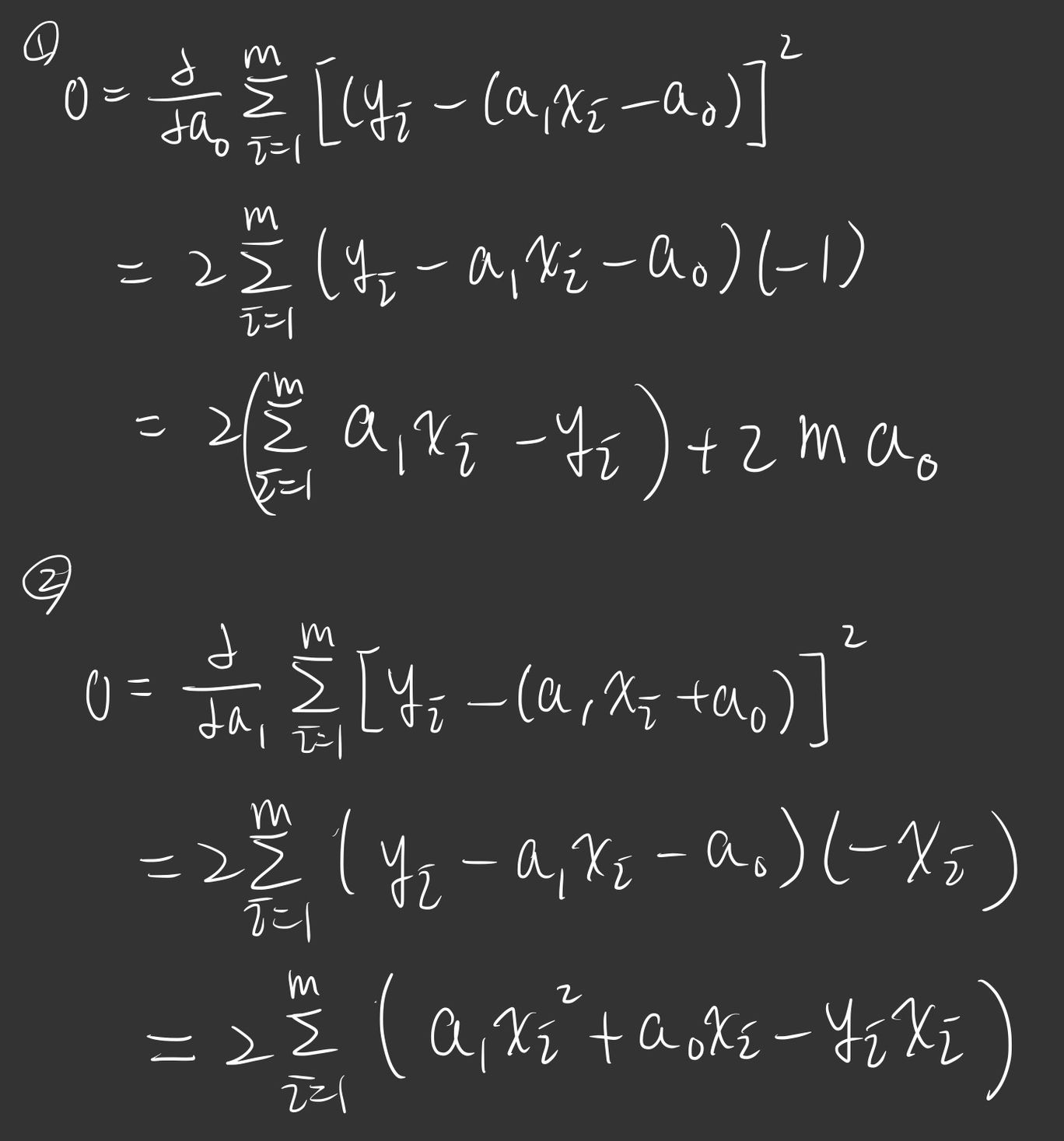
然後我們可以推出(用克拉瑪)：

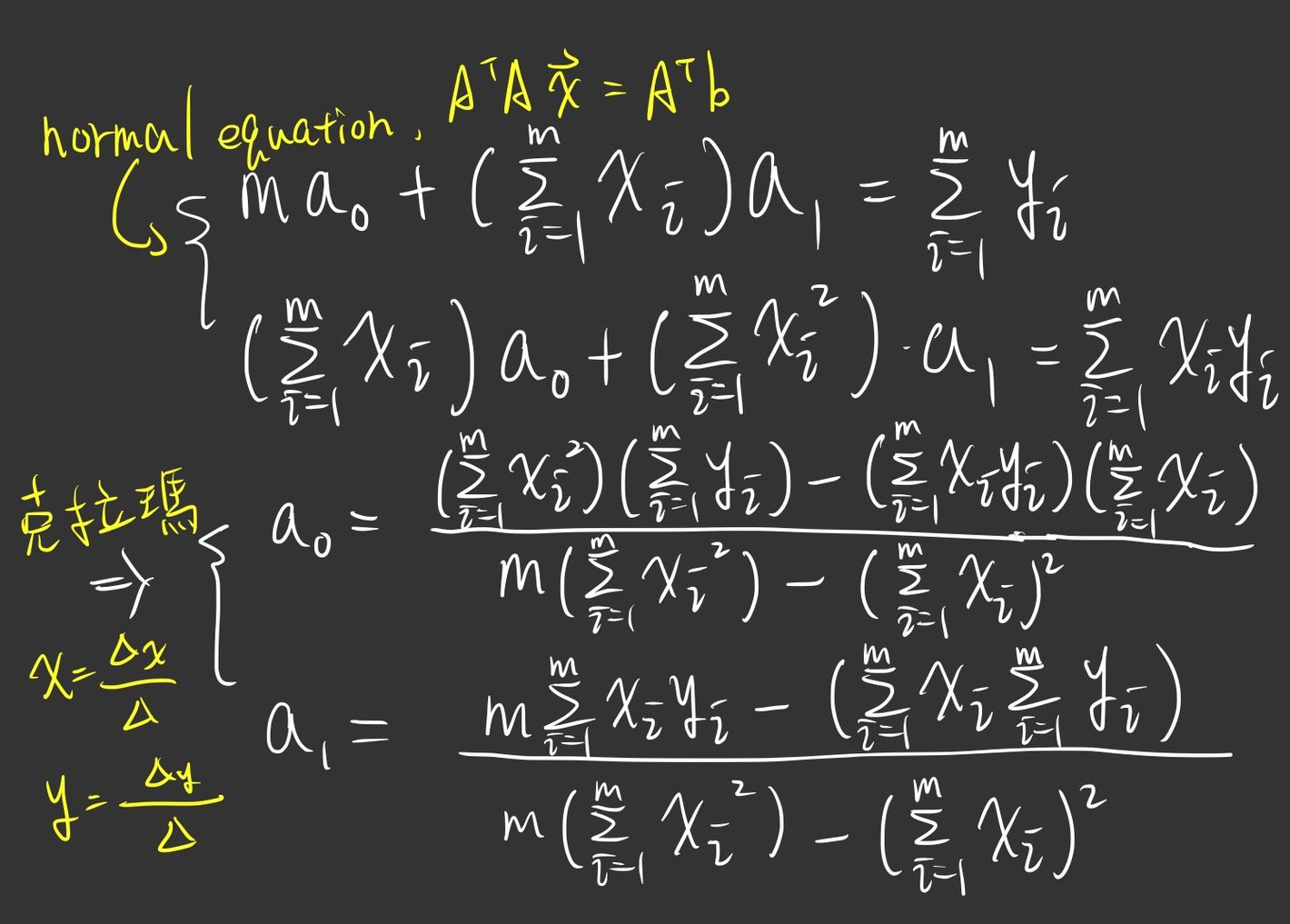
這兩個等式就叫 normal equation

Polynomial Least Squares

然而妳拿到的資料很有可能不是一個用 $a x + b$ 就能表達的資料分布，像是這樣：

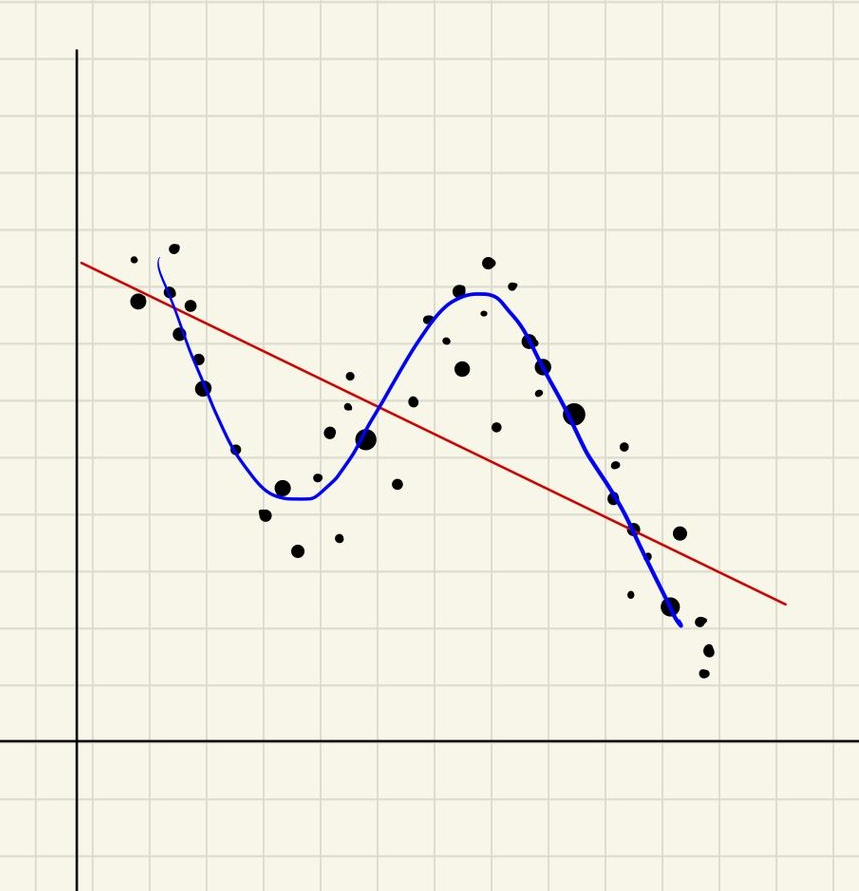
藍線明顯比紅線更好的講述了這個資料的分布，要做出這種藍線，我們就需要用更高次方的多項式來表達他，這時就需要用 Polynomial Least Squares 了

我們假設

$P_{n} (x) = a_{n} x^{n} + a_{n - 1} x^{n - 1} + . . . + a_{1} x + a_{0}$ ，defree n < m - 1

那我們要找到 $a_{0}, a_{1}, . . ., a_{n}$ 來最小化 E：

那一樣對他偏微：

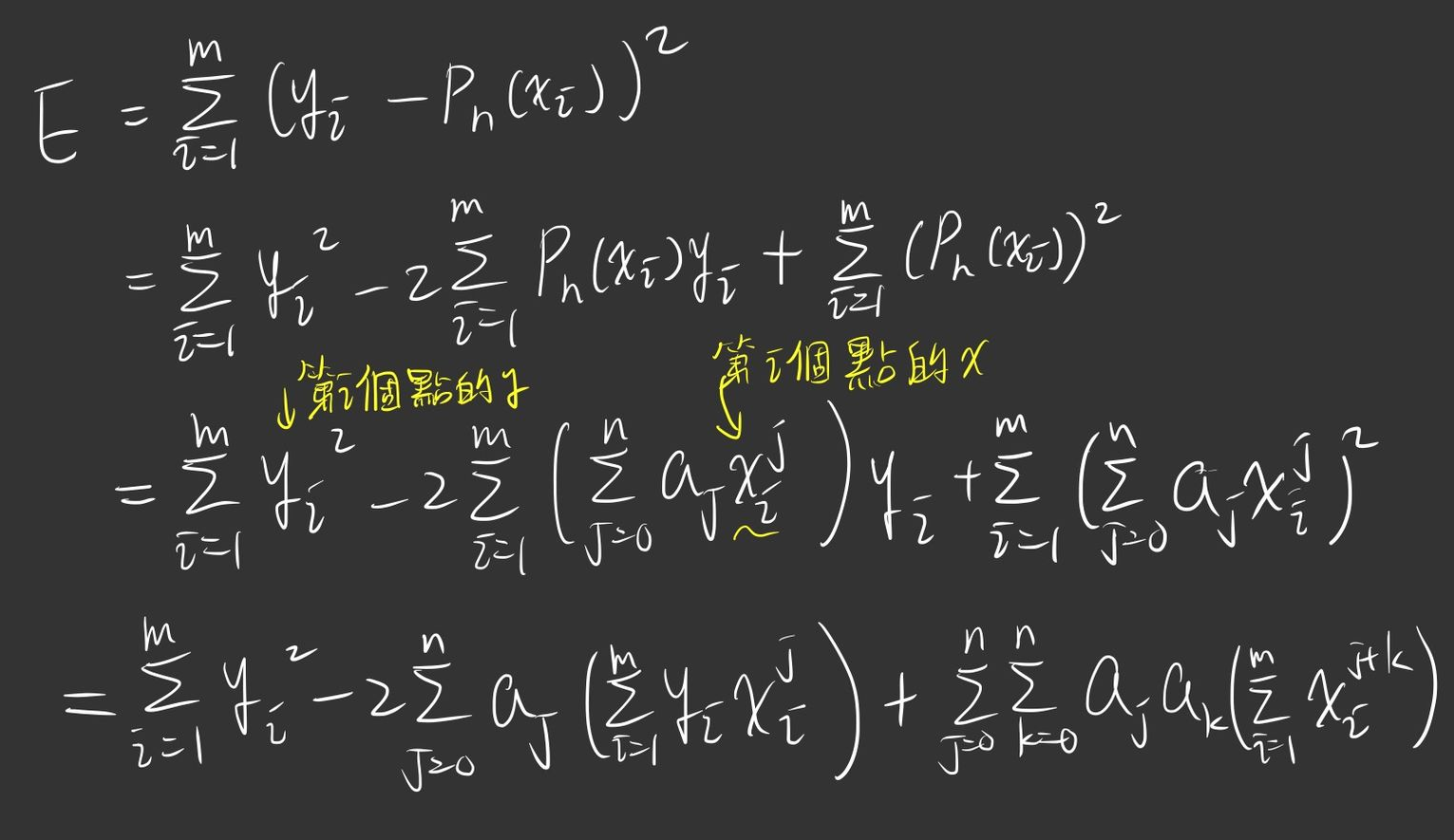
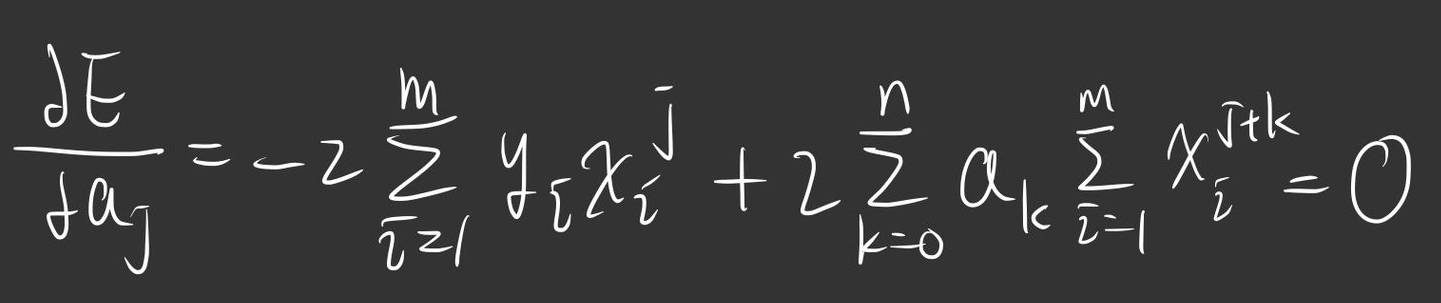
那我們就可以推出這樣：

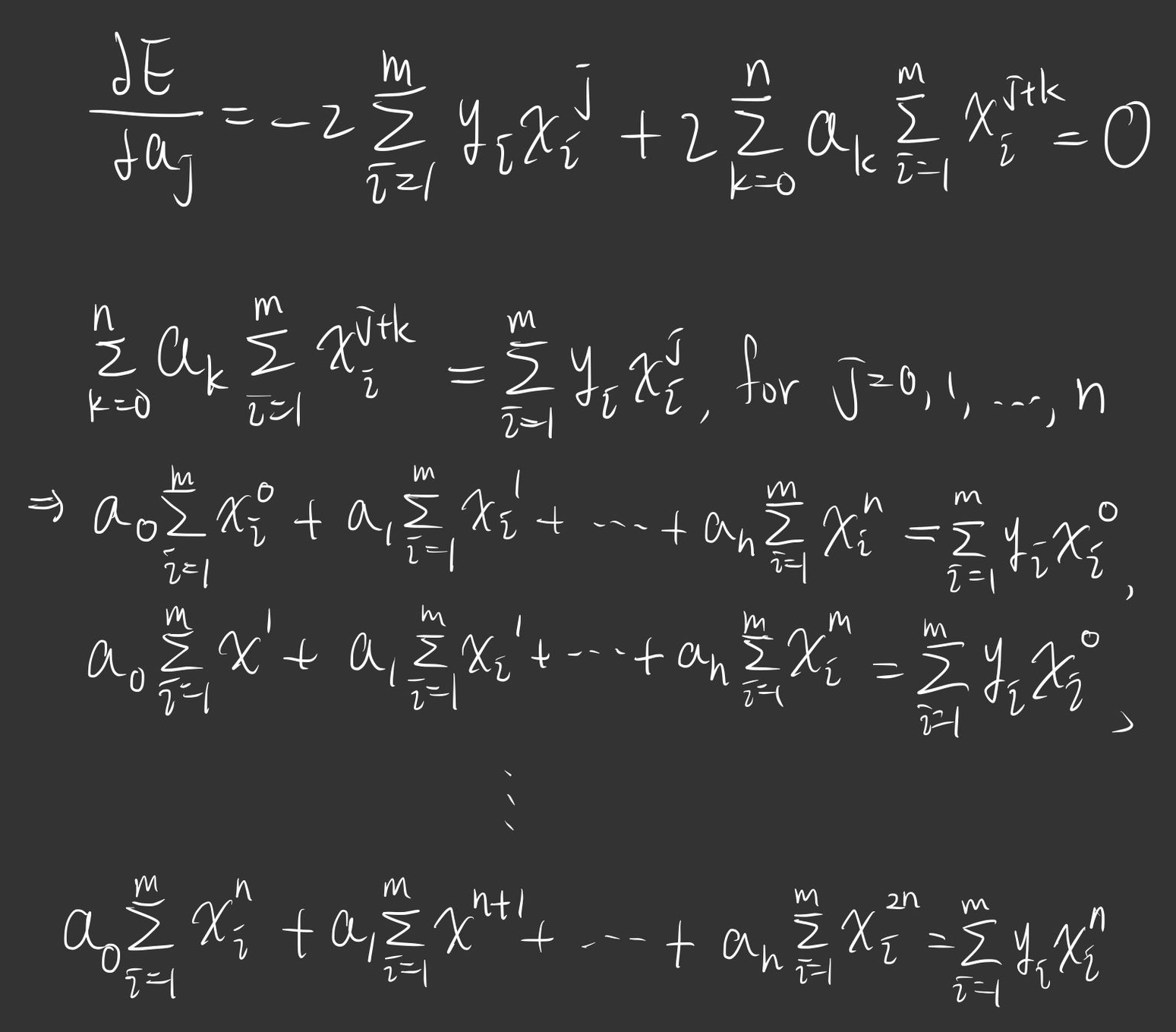
用矩陣表示

我們的目的是找到一條線 $y = a_{1} x + a_{0}$ ，或一個曲線，可以很好的表示資料 ${(x_{i}, y_{i})}_{i = 1}^{m}$ 的走向，後面可能會用 b 來代表 $a_{0}$ ，畢竟比較習慣用 b 來寫

寫成矩陣會像這樣：

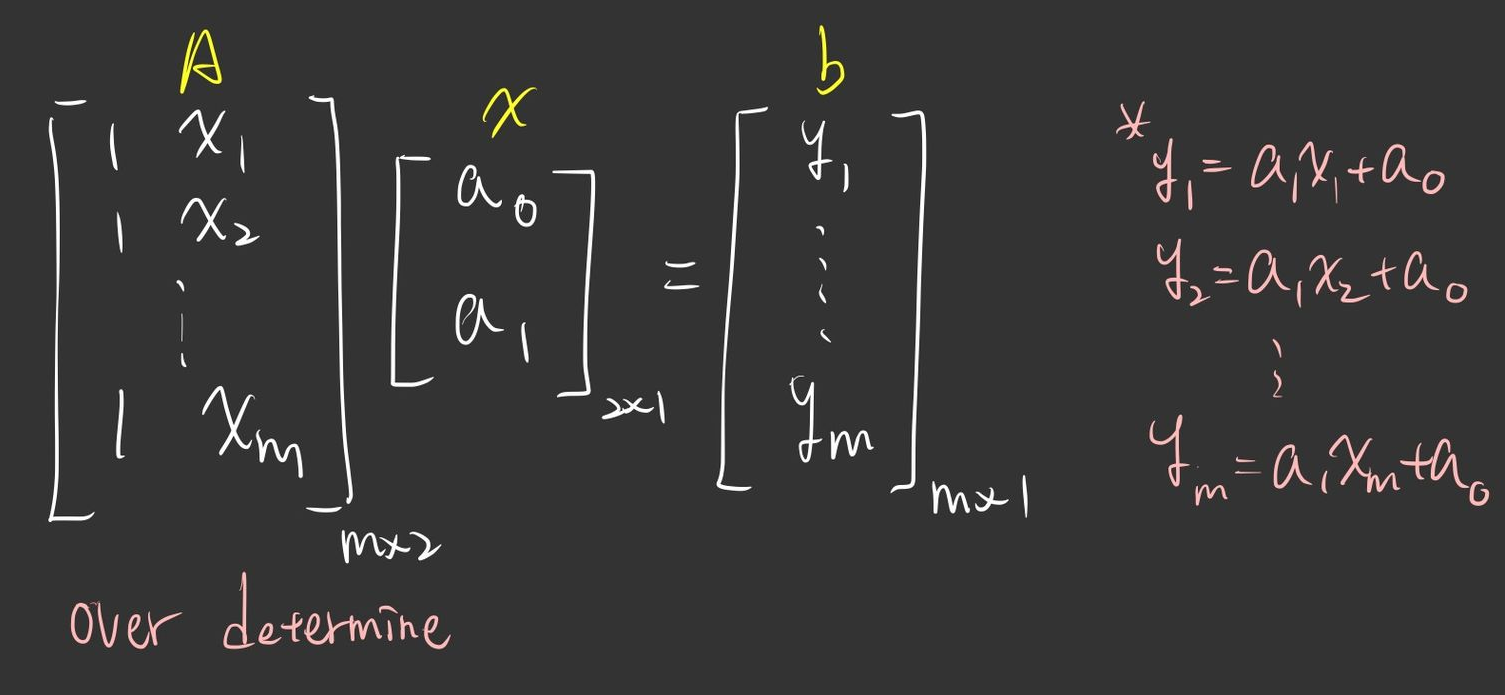
但通常 $b \notin C (A)$ ，所以我們改成去找能讓 residual $E (\vec{x}) = | | \vec{b} - A \vec{x} | |_{2}$ 最小化的 $\vec{x}$ 。假設 $A \in R^{m \times n}, b \in R^{m + 1}$ ，其中 $m > n$ (under determine)，

那麼 $\vec{x}$ 最小化 $E (\vec{x}) = | | \vec{b} - A \vec{x} | |_{2}$ iff $\vec{x}$ 是 $A^{T} A \vec{x} = A^{T} \vec{b}$ 的解

證明：

這裡的 $\vec{y}$ 是 $R^{n \times 1}$ 裡的隨便一個向量， $A$ 作用上去就會變 $C (A)$ 裡面的一個向量，所以和 $b - A \vec{x}$ 內積就會等於 0，因為垂直

註： $A \vec{x}$ 解出來的所有結果會在一個固定的區域中，這個區域就叫作 column space $C (A)$ ，顧名思義就是每個 column 的線性組合 ${\vec{a}}_{0} + {\vec{x}}_{1} {\vec{a}}_{1} + {\vec{x}}_{2} {\vec{a}}_{2} + . . . + {\vec{x}}_{m} {\vec{a}}_{m}$ ，一維的話就是一條線，二維的話就是一個平面

那這個東西解起來就會像這樣：

因為我們拿到的資料通常都不會在平面 $C (A)$ 上，也就是剛剛說的通常 $\vec{b} \notin C (A)$ ，尤其是在妳資料點很多的時候 A 就會很長一坨，像上面就有 m 個資料點，所以 A 就是個 $m \times 2$ 的矩陣，如果 m 遠遠大於 2，那 $A \vec{x} = \vec{b}$ 基本上都沒有解，所以我們才會在這邊用這個方法找到誤差最小的解

多維的 normal equation

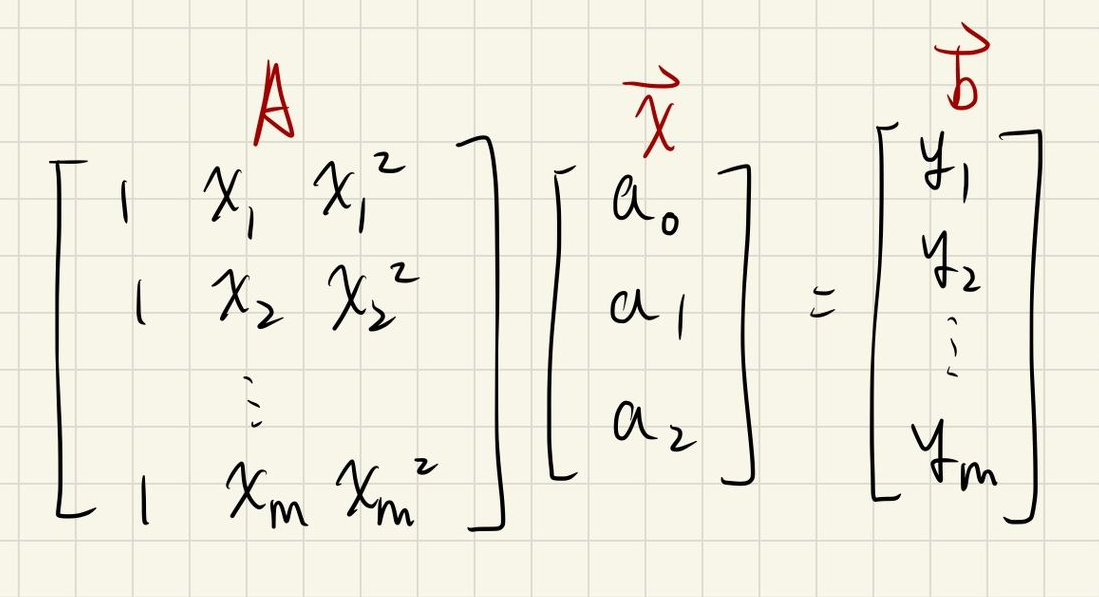
多維代表不只有 $a_{0}$ 、 $a_{1}$ ，還有其他的 $a_{2}$ 、 $a_{3}$ 等等，所以你的 $A$ 的 column 數就會增加，以 $y = a_{2} x^{2} + a_{1} x + a_{0}$ 來說就會長這樣：

那麼 $\vec{x} = (A^{T} A)^{- 1} A^{T} \vec{b}$ 大家應該就會求了

自然對數相關

有時候資料的表示式可能是 $y = b e^{a x}$ 這類的形式，那麼我們可以這樣寫：

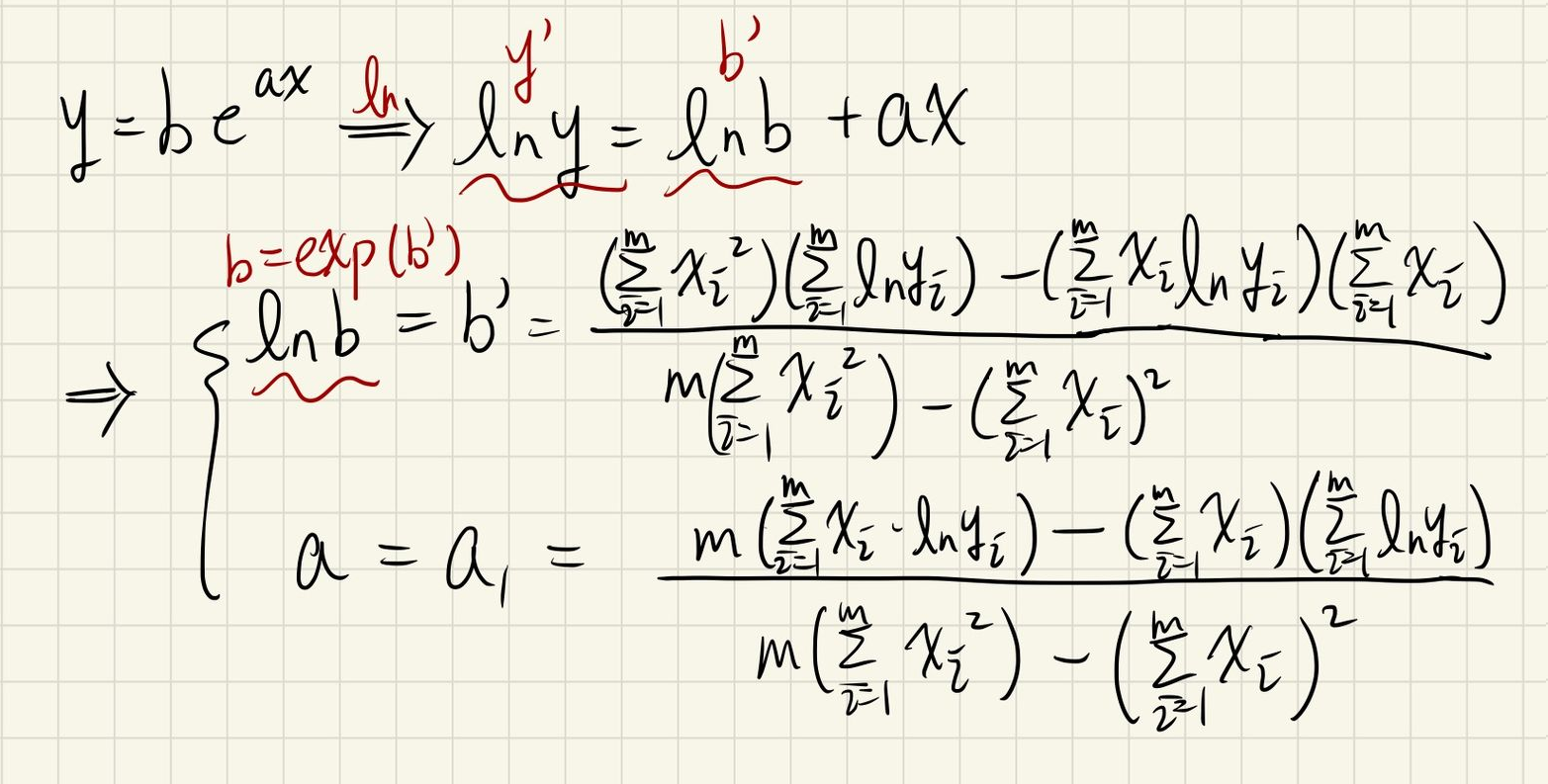
基本上跟前面講的一樣