Gauss-Seidel Metheod

Gauss-Seidel Metheod

上次我們用了 Jacobi's method，它操作起來長這樣：

然後我們就發現 ${\overrightarrow{x}}^{(k)}$ 裡的元素 ${\overrightarrow{x}}_1^{(k)}$, ${\overrightarrow{x}}_2^{(k)}$, ... , ${\overrightarrow{x}}_{i-1}^{(k)}$ 都已經被算出來了，那因為 ${\overrightarrow{x}}_j^{(k)}$ 會比 ${\overrightarrow{x}}_j^{(k-1)}$ 更準更接近解，所以我們可以把上面的公式換成這樣：

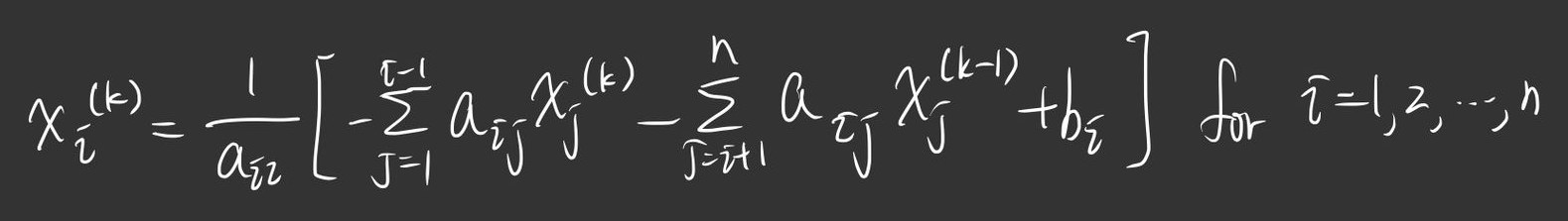
可以看見我把公式拆成了兩部分，前面那邊是已經算出來的，後面的是還沒算到的，以上面 ${\overrightarrow{x}}_3^{(k)}$ 的例子來說，${\overrightarrow{x}}_1^{(k)}$、${\overrightarrow{x}}_2^{(k)}$ 就是已經算出來的，${\overrightarrow{x}}_3^{(k)}$、...、${\overrightarrow{x}}_n^{(k)}$ 就是還沒算出來的值

這個方法我們就稱它為 Gauss-Seidel Method，是一種 Jacobi's 的優化

Gauss-Seidel Metheod 的矩陣表示法

上次我們把原本的矩陣分成 D、L、U：

那我們做了優化之後，可以把它寫成這樣：

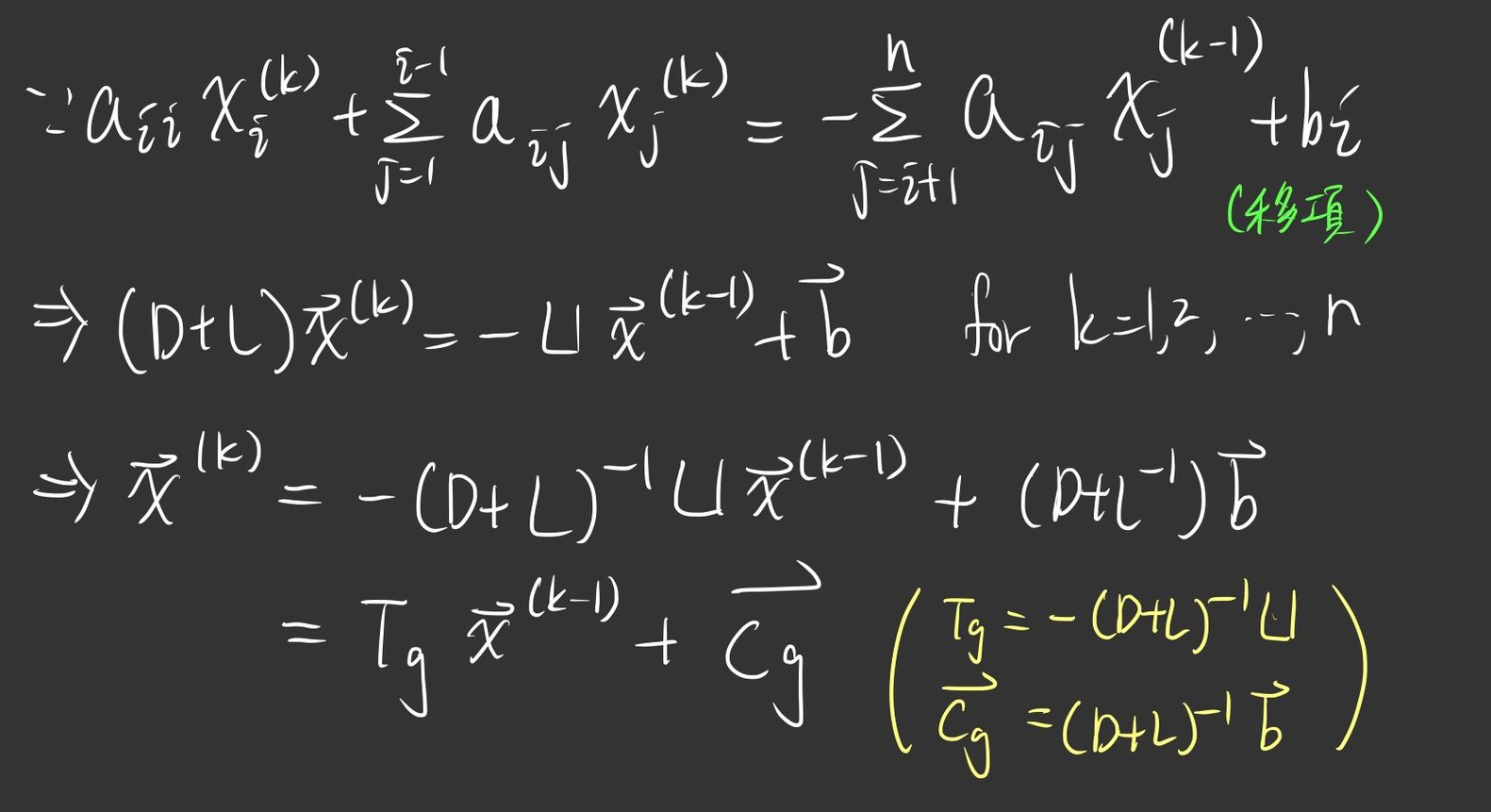
那一樣我們要讓電腦去跑，所以寫個 pseudocode

輸入(input)：n、矩陣A、rhs 向量 $\overrightarrow{b}$、初始猜測值(initial guess) $\overrightarrow{x_0}$、誤差(tolerance) TOL、最大跌代次數 $N_0$

輸出：估計出來的 $\overrightarrow{x}$

::

Lemma7.18

如果 T 的譜半徑($\rho (T)$) 小於 1，那麼會存在 $(I-T{)}^{-1}=I+T+T^2+...={\mathrm{\Sigma }}_{j=0}^{\mathrm{\infty }}{T}^j$

你可以把它想像成一個公比小於 1 的等比數列 $x^j$，那麼它的和就是 ${\mathrm{\Sigma }}_{j=0}^{\mathrm{\infty }}{x}^j=1+x+x^2+...=\frac{1}{1-x}$

證明：

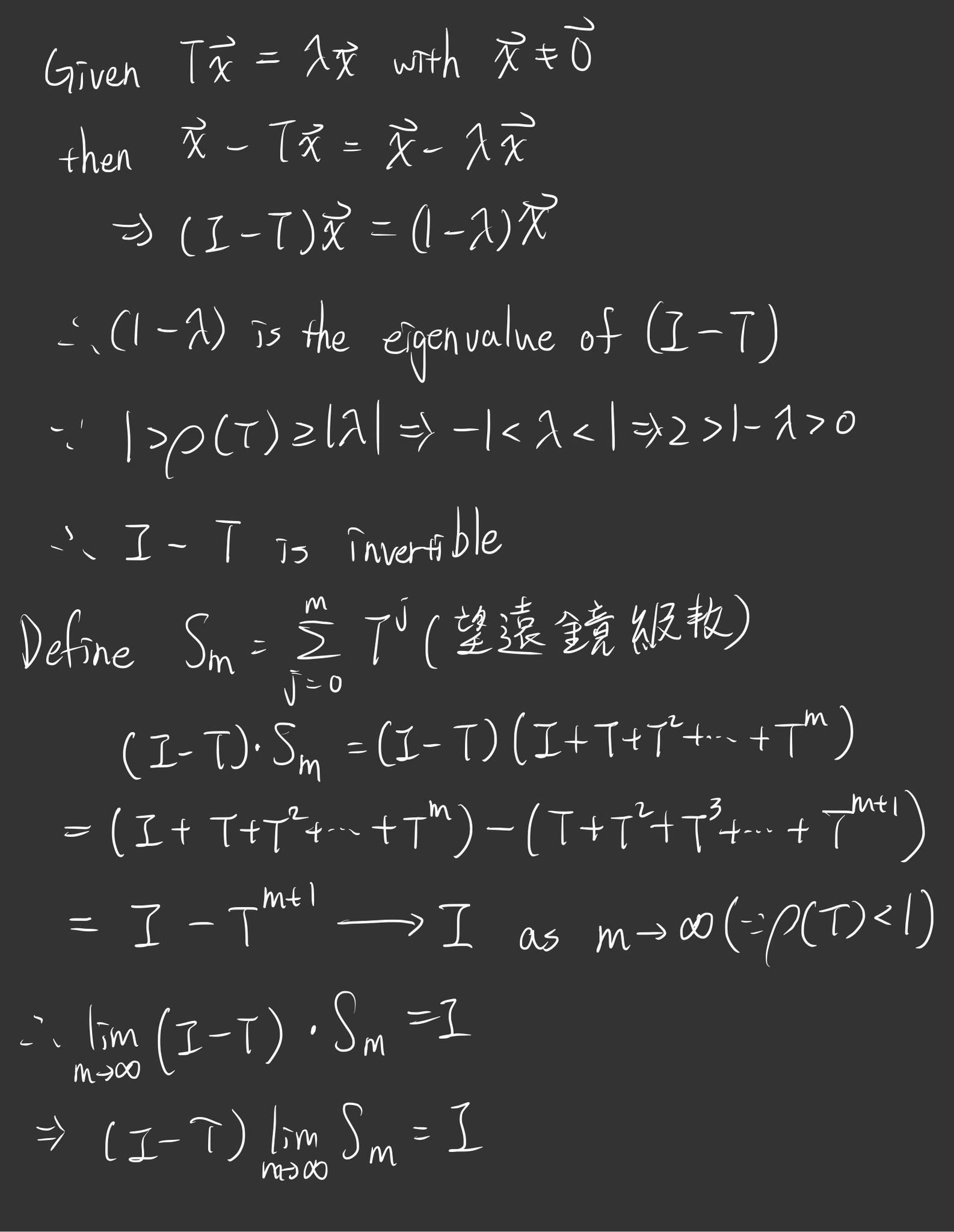
Thm 7.19

隨便猜一個初始值 ${\overrightarrow{x}}^{(0)}$，定義為 ${\overrightarrow{x}}^{(k)}=T{\overrightarrow{x}}^{(k-1)}+\overrightarrow{C}$ for $k\ge 1$ 的數列 $\{{\overrightarrow{x}}^{(k)}{\}}_{k=0}^{\mathrm{\infty }}$ 會收斂到某個特殊的解 $\overrightarrow{x}=T\overrightarrow{x}+\overrightarrow{C}$ iff $\rho (T)<1$

證明：