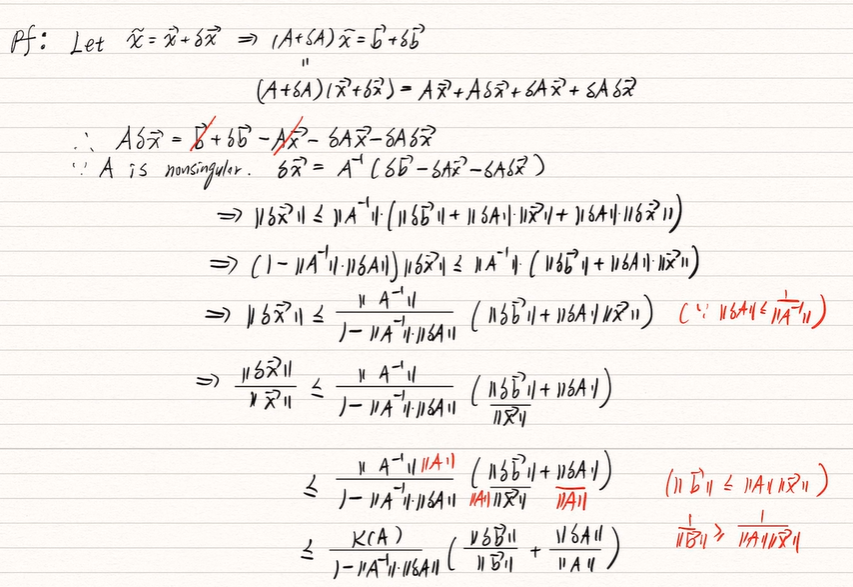Error Bounds

電腦裡面要表達一個數字，像是 $\pi$，是無法沒有誤差表達出來的。在電腦裡面我們能表達的數大概在 ${10}^{-300}$ ~ ${10}^{300}$ 之間

所以你也可以知道如果我們要電腦幫我們解 Ax = b，那麼必定會有誤差，因為電腦除了整數之外，大部分的數字是幾乎不可能沒有誤差的

Def

我們要解 Ax = b 這個線性系統的時候，假設我們透過迭代方法找到一個解 $\overline{x}$，那我們當然期望 $\overline{x}$ 和 x 之間的距離要非常接近

如果現在只有 $\overline{x}$，很明顯 $A\overline{x}$ 不會等於 b，那我們就定義一個東西叫 residual vector $\overrightarrow{r}=\overrightarrow{b}-A\overline{x}$，residual 就是殘餘的意思

那我們就期待如果 $||\overrightarrow{r}||=||\overrightarrow{b}-A\overline{x}||$ 很小，那麼 $||\overrightarrow{x}-\overline{x}||$ 就會很小。 你可能會想說這很理所當然，但針對某些線性系統這會不成立，也就是說雖然 $||\overrightarrow{r}||$ 很小，但 $||\overrightarrow{x}-\overline{x}||$ 卻很大，因為電腦並沒有辦法準確的表達所有數字

我們看個例子，這邊我們解一個 Ax = b：

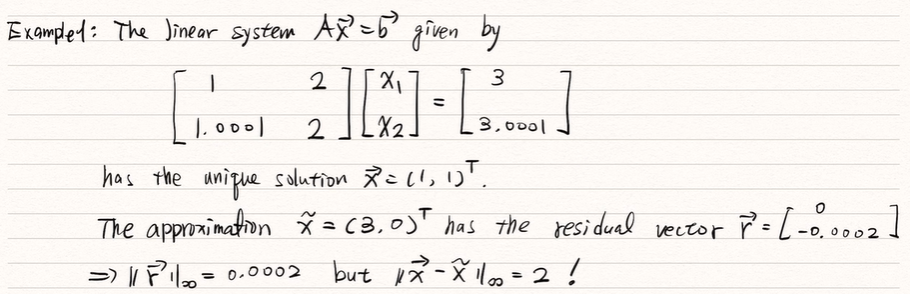
A 矩陣的第一個 row 和第二個 row 只有一點點差異，如果我們用手去解你會發現他是可逆的，然後解會是 $\overrightarrow{x}=(1,1{)}^T$

但如果我們今天用某種迭代方法算出一個解長 $\overline{x}=(3,0{)}^T$，你把它丟進去算 residual vector，然後算 infinity norm，他會是 0.0002，但你去算 $||\overrightarrow{x}-\overline{x}|{|}_{\mathrm{\infty }}$ 卻會是 2

那為什麼，原因完全出現在 A 矩陣裡面，我們接 Thm 7.27

Thm 7.27

我們假設 $\overline{x}$ 是一個 Ax = b 的逼近解且 A 是 nonsingular，那我們會發現 $||\overrightarrow{x}-\overline{x}||\le ||\overrightarrow{r}||\cdot ||A^{-1}||$

然後如果 $\overrightarrow{x}$ 不是 trivial 的解且 b 不是 0 向量，那我們可以導出這件事來(我全貼) ：

我們先看一下上面的在說什麼，他的意思是逼近解跟真實解的絕對誤差會小於等於右邊那個東西，而下面那個則是逼近解與真實解的相對誤差會小於等於右邊那個式子

所以一個是絕對誤差，一個是相對誤差

套用到剛剛的例子，就會長這樣：

也就是說雖然 $||\overrightarrow{r}||$ 很小，但 $||A||\cdot ||A^{-1}||$ 很大的話仍然會爆掉：

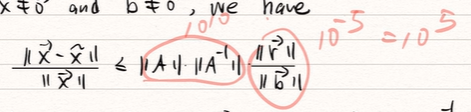
所以關鍵就是在 $||A||\cdot ||A^{-1}||$

證明：

Def 7.28

$||A||\cdot ||A^{-1}||$ 在線代裡面是個很重要的東西叫做條件數(condition number)，記做 K(A)

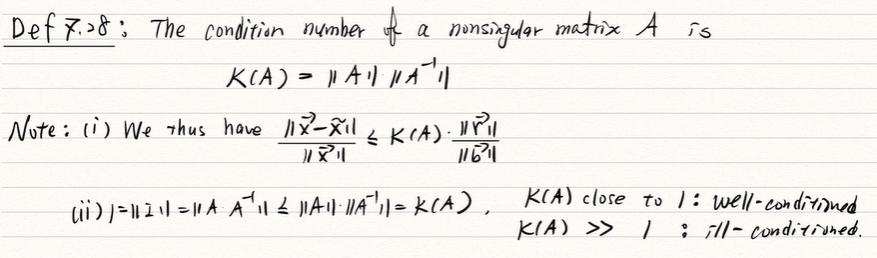
如果 K(A) 接近 1，我們就說這個系統是良置的，如果遠遠大於 1，就說這個系統是病態的

舉個例子：

Thm 7.29

接下來是另一個主題，就像一開始所說我們會有 rouding error，又稱 perturbation，也就是說我們實際上 Ax = b 丟進去電腦時會跑出個 $\delta$，像這樣：

那我們把它就代回 Ax = b：

這時我們就會發現電腦裡面算出來的 $\overline{x}$ 和我們實際上的 x 的相對誤差是上圖下面那樣，一樣取決於 K(A)

證明：