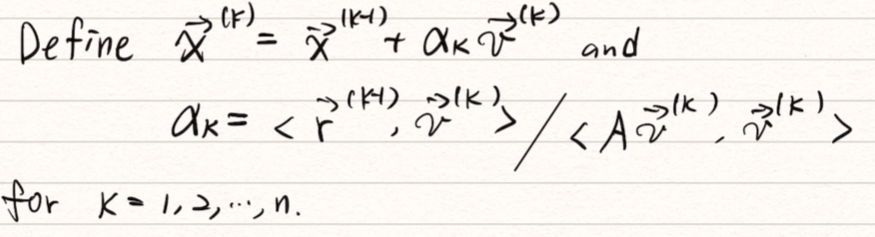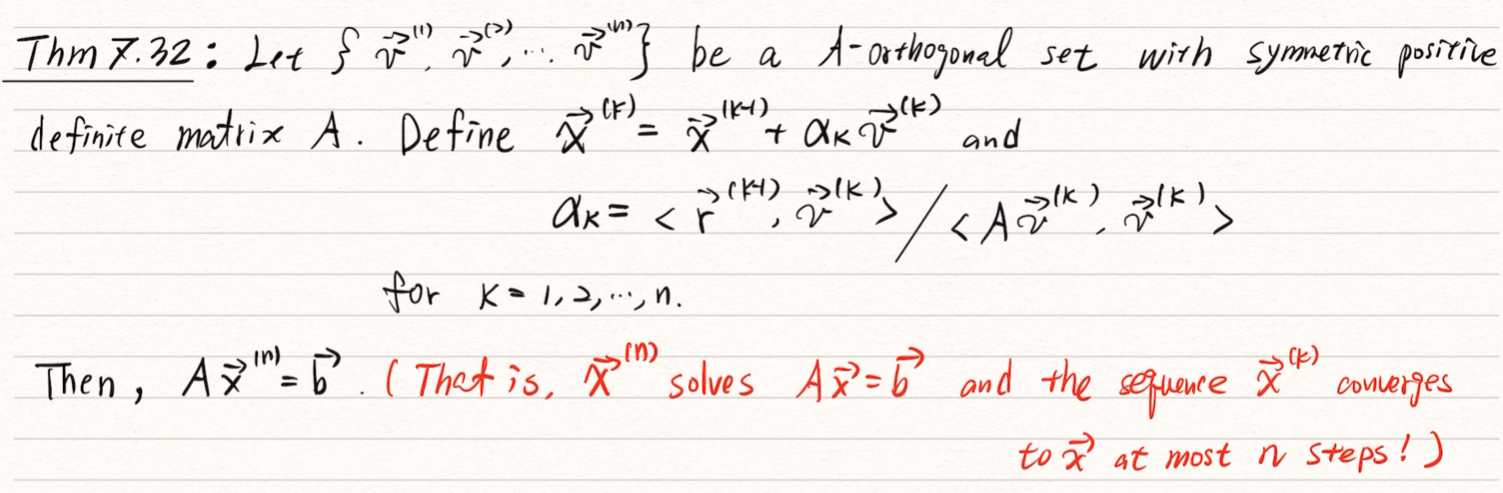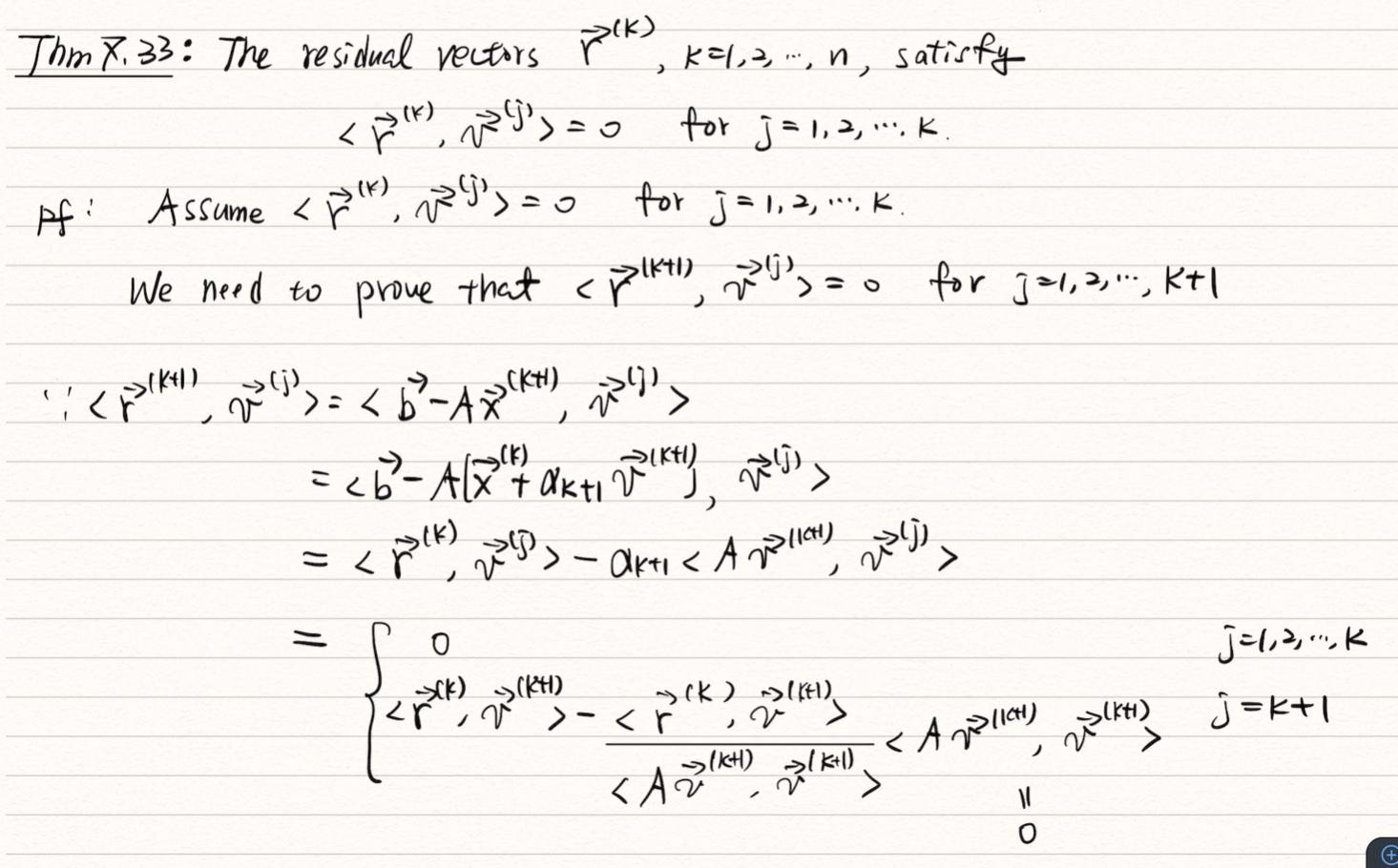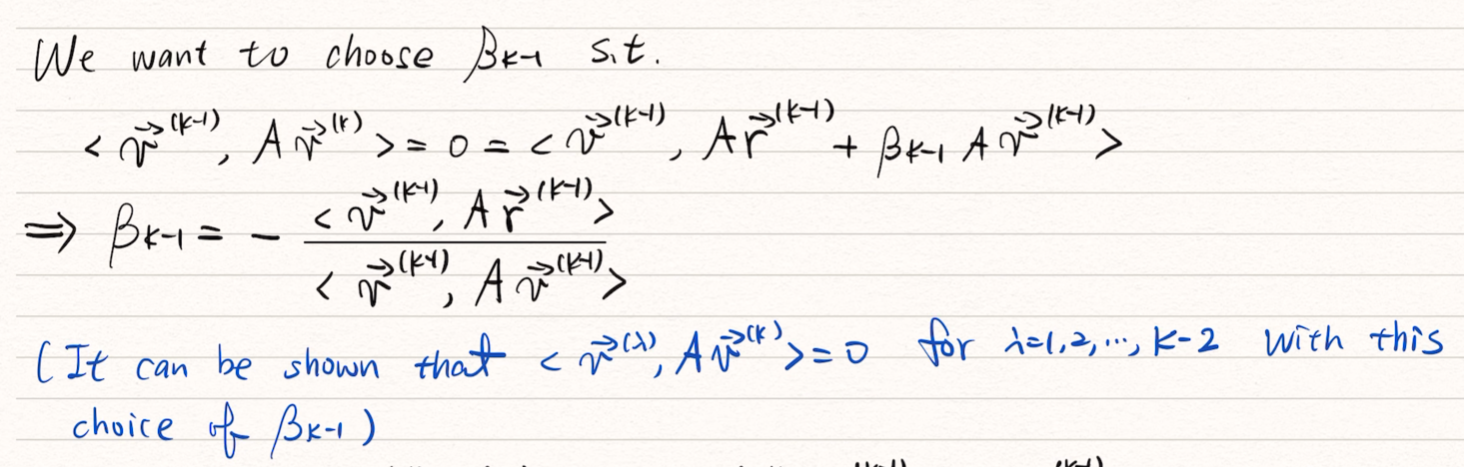Conjugate Gradient Method

這邊我們一樣考慮解 $A \vec{x} = \vec{b}$ ，前面講的是 Gradient Method，那這節要講的是 Conjugate Gradient Method，效率一般來說會更好，而且好很多

$α$ 要選來 minimize $Φ ({\vec{x}}^{(k)})$ ，因為我們希望它越小越好，前面的 Gradient Method 裡面 ${\vec{p}}^{(k - 1)}$ 是用 gradient 來做的，但這邊我們不用這個方法

我們先看 $α$ ，先不管 ${\vec{p}}^{(k - 1)}$ ，所以假設 ${\vec{p}}^{(k - 1)}$ 已知：

基本上推導過程差不多，所以重點就是 ${\vec{p}}^{(k - 1)}$ 要怎麼找

A-orthogonal

在開始找之前我們先給個定義，假設 A 是個 $R^{n \times n}$ 的矩陣，我們說有一個 nonzero vector 的 set ${{\vec{v}}^{(1)}, {\vec{v}}^{(2)}, . . ., {\vec{v}}^{(n)}}$ ，如果這個集合滿足 $< {\vec{v}}^{(i)}, A {\vec{v}}^{(j)} >= 0 i f i \neq j$ 的話，我們就說這個集合是一個 A-orthogonal 的 set

那我們說這個集合如果是 A-orthogonal 而且 A 矩陣是對稱正定的話，那麼這個集合必定會線性獨立，證明：

代表這個集合是 $R^{n}$ 的一組基底

Thm 7.32

給定一個集合 A-orthogonal 的集合 ${{\vec{v}}^{(1)}, {\vec{v}}^{(2)}, . . ., {\vec{v}}^{(n)}}$ ， $A$ 是對稱正定矩陣

那當我們要解 $A \vec{x} = \vec{b}$ 時我們要用這個式子：

那妳可以看見 $\vec{v}$ 只有 n 項，也就代表最多只會迭代 n 次，也就是說 ${\vec{x}}^{(n)}$ 就是我們要的 $\vec{x}$

證明：

所以現在問題就變成 $\vec{v}$ 要怎麼找了

Thm 7.33

residual vector ${\vec{r}}^{(k)}$ , k = 1, 2, ..., n，滿足 < ${\vec{r}}^{(k)}, {\vec{v}}^{(j)}$ > $= 0$ , j = 1, 2, ..., k

也就是說 ${\vec{r}}^{(1)}$ 和 ${\vec{v}}^{(1)}$ 垂直， ${\vec{r}}^{(2)}$ 和 ${\vec{v}}^{(1)}$ 還有 ${\vec{v}}^{(2)}$ 垂直， ${\vec{r}}^{(n)}$ 和全部的 ${\vec{v}}^{(j)}$ 垂直

那證明我們就用數學歸納法：

找 A-orthogonal 的集合

假設執行到第 k 步的時候 ${\vec{x}}^{(1)}, {\vec{x}}^{(2)}, . . ., {\vec{x}}^{(k - 1)}$ 且 ${\vec{v}}^{(1)}, {\vec{v}}^{(2)}, . . ., {\vec{v}}^{(k - 1)}$ 都已經知道了，那下一次的 ${\vec{v}}^{(k)} = {\vec{r}}^{(k)} = {\vec{r}}^{(k - 1)} + β_{k - 1} {\vec{v}}^{(k - 1)}$