Games101:Rasterization (光柵化)
Games101:Rasterization (光柵化)
在 MVP Transformation 一節中我們已經介紹了要如何將整個坐標系投影的螢幕坐標上,同時也先簡單介紹了螢幕空間,如果你還不曉得這些是什麼,那記得先去看前一節
這些轉換後得到的信息此時還只是空間中描述的一堆三角形,還沒有真正的變成圖片,因此這節我們就要講如何讓它變成圖片,也就是要怎麼將這些空間中的三角形轉化成像素,將多邊形打碎成像素的過程就是我們所說的光柵化
CRT 螢幕
早期的 CRT 螢幕內使用陰極射線管,其會產生很多的電子,這些電子在經過加速後,會穿過顯示設備,並發生偏轉,進而打在螢幕上的某一個位置。 如果這個過程足夠快,你就不會看到一個一個電子打在螢幕上的過程,而是會看到一整個形狀,這就是早期 CRT 螢幕的原理:
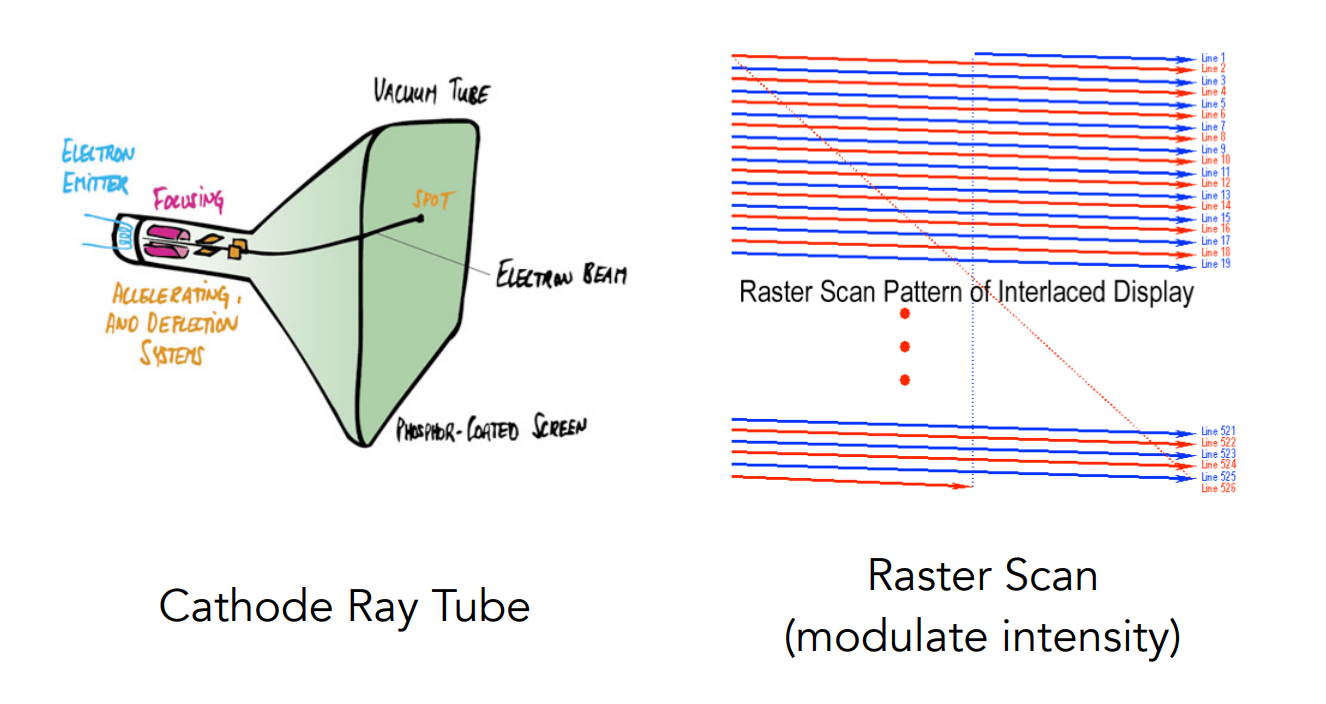
這些電子在打的時候是通過一種類似掃描的方式,從左上角開始往右填滿一整個 row,接著換到下一列再重複這個動作,當這些線足夠密集的時候就可以覆蓋整個螢幕了
有時候為了畫快一點,每張圖像上可以只挑選奇數或偶數行畫,例如第一張圖只畫奇數行,第二張圖只畫偶數行,如此交替,由於人眼的視覺暫留,看起來就與全畫差不多,不過這對於一些高速運動的畫面會有撕裂感。 這個做法被稱為隔行掃描,現今仍有一些壓縮技術在使用
三角形
前面有提到我們基本上是用三角形在表示物體的,這是因為三角形的表現能力很強,也有很多不錯的性質,例如它是最基礎的多邊形,沒有比三角形邊更少的多邊形了,否則就退化為線段了;再來所有的多邊形都可以被拆成三角形,因此三角形相當於是所有多邊形的基礎
還有,如果我們給定三角形的三個點,連成了一個三角形,其內部一定會是個平面;如果是四邊形,想像沿著某個對角線一折,它就不是平面的了,但三角形不會,除非你把它折成兩個三角形。 而且三角形的內外定義是非常清晰的,我們可以通過向量的外積來判斷一個點是不是在三角形內的
另外,假設三角形的三個頂點有不同的屬性,那在三角形內,我們是可以透過內插來達到漸變的效果的,也就是可以把三角形內任何一個點的屬性給猜出來
Sampling introduction (取樣/採樣)
所以我們現在就盯著三角形來看,我們知道不管原先的三角形在哪裡,經過 MVP 和 Viewport 變換後現在都在螢幕座標中,透過其
現在看左邊這幅圖,它是一個三角形,三個頂點的座標我們都可以寫出來,現在我們想要把三角形給變成真正的像素
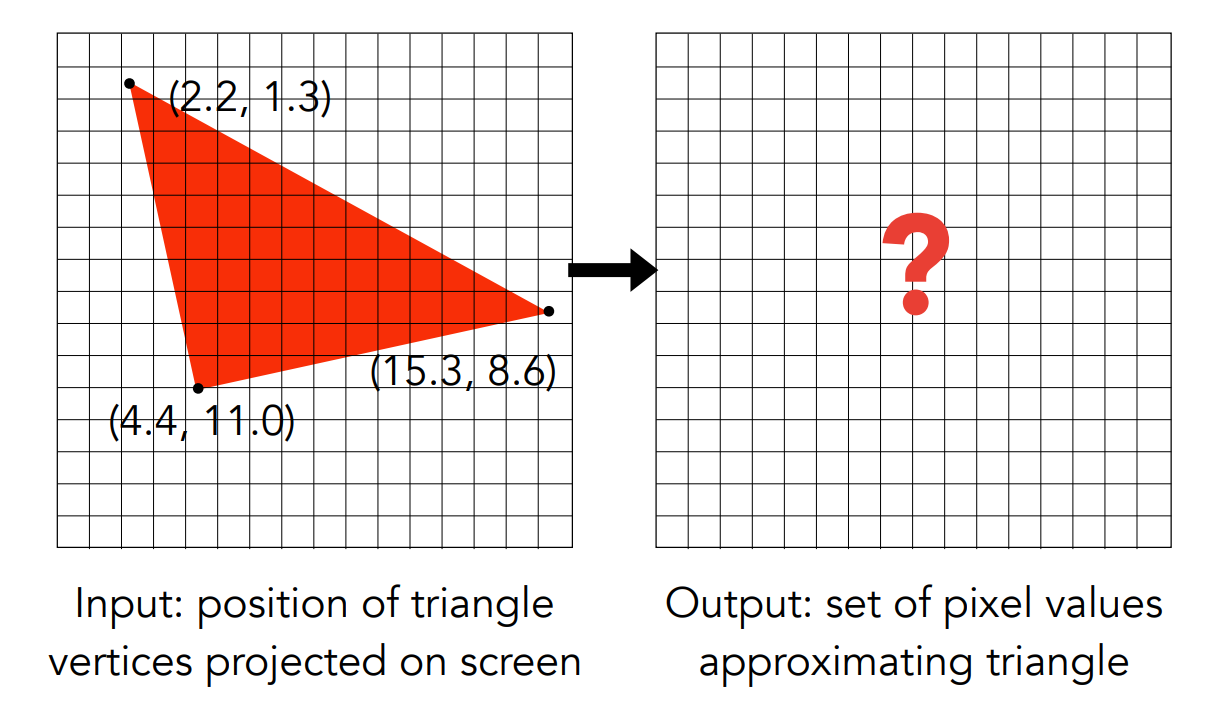
Info
圖中的坐標系原點是在左上角,但這沒關係,不影響我們解釋概念
但像素的內部是不可能有顏色變化的,整個像素需要維持同一個顏色,因此像是底下這種情況:
它剛好被三角形擋住了大約一半的面積,那這個到底要怎麼算呢? 它只能是全紅或是全白的,如何判斷這種情況就是接下來我們要做的事情,也是光柵化中最重要的一個概念 ── 取樣
所謂的取樣簡單來說就是,給你一個連續的函數,我們在不同的地方去取這個函數的值是多少,假設有一個函數
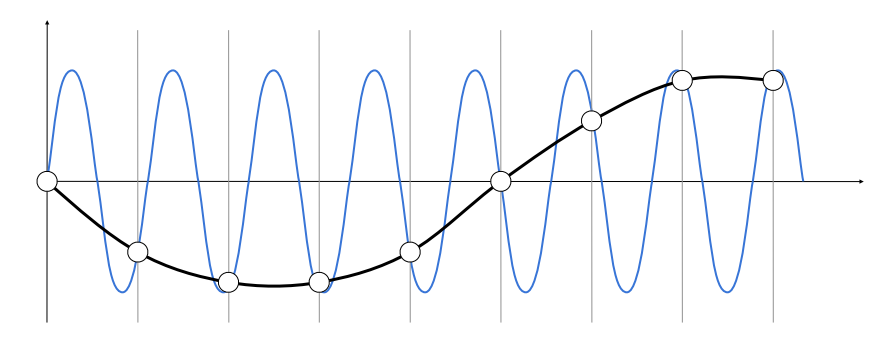
在圖學中這是一個很重要的概念,我們會涉及到各種不同的取樣,我們需要利用像素的中心對螢幕空間進行取樣,這相當於我們需要算出一個定義在螢幕空間上的函數,在不同的像素中心的值是多少
後面我們還會提到可以對時間、位置取樣,又或是物體表面反射的性質也可以取樣,甚至是三維空間本身也可以取樣,例如醫學中的 CT 或是核磁共振成像等,成像的結果是三維的,這就是對病人體內位置的取樣結果
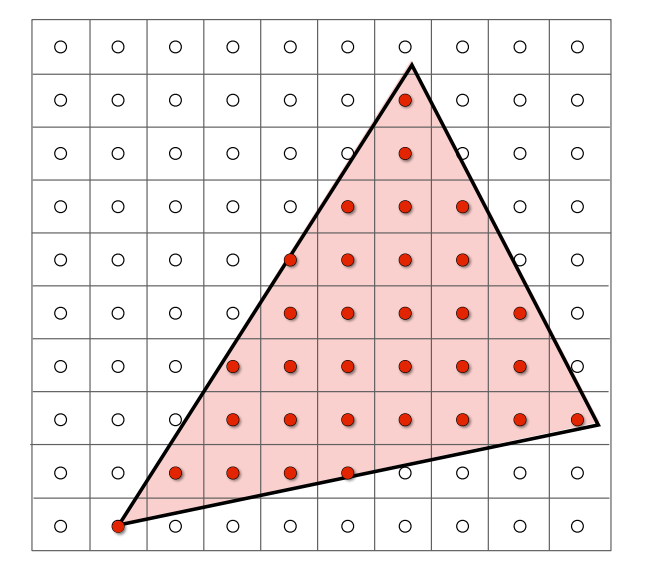
回到我們的例子中,我們要取樣的是一個三角形,我們可以透過判斷像素的中心是否在三角形內來進行取樣,這個操作可以寫成函數 inside:
應該沒什麼問題,如果點在三角形內就回傳
接下來我們可以透過遍歷整個螢幕空間來去檢查所有的像素中心是不是在三角形內:
for (int x = 0; x < xmax; ++x)
for (int y = 0; y < ymax; ++y)
image[x][y] = inside(tri, x + 0.5, y + 0.5);之後再給它不同的顏色,這就是一個最最最簡單的通過取樣方法來完成的光柵化過程
如何判斷在三角形內?
接下來我們要考慮如何實作 inside 函式,這個問題前面已經提到可以用外積來做了,假設如下圖,給予三角形的三個頂點
計算
接著我們繼續計算
這邊拿一下 GAMES103 的投影片來幫助理解:
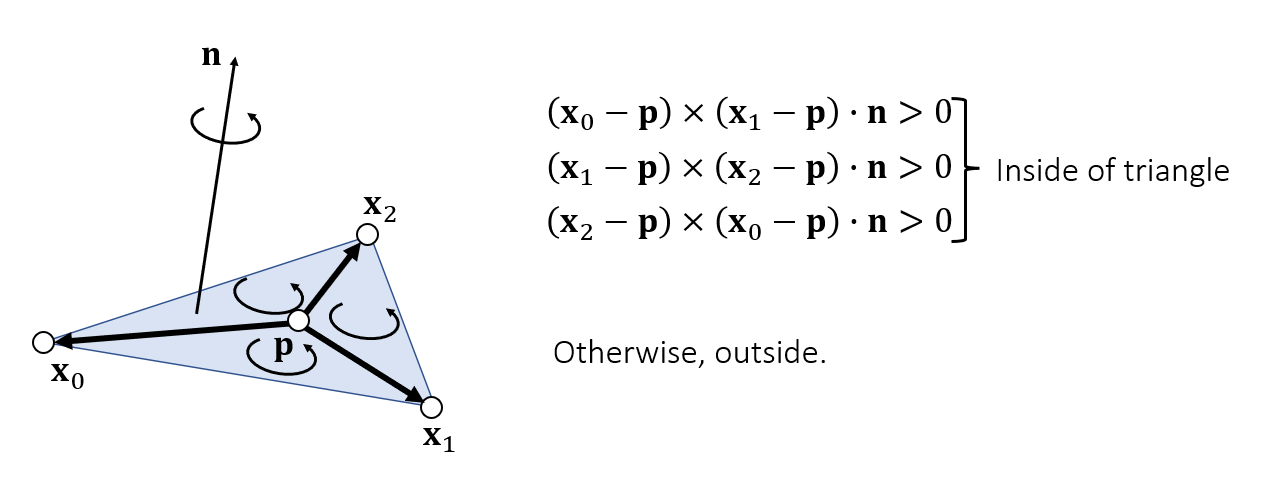
至此,我們就知道給定一個點與一個三角形,該如何判斷點是否在三角形內了,接著只要結合前面取樣的方法,就可以知道每一個像素對應的值了
到這邊你可能會有一個問題,如果點剛好在邊上怎麼辦? 通常對於這類邊界問題,圖學中常常會選擇忽略它,因此這邊我們就先不做處理,不過在一些圖學的 API 內,例如 OpenGL 或 DirectX,它們有對應的嚴格定義,有興趣的可以再去查查看
Aliasing (混疊/走樣)
現在我們按照上面的方法將三角形投影到像素上了,此時它的樣子會長這樣:
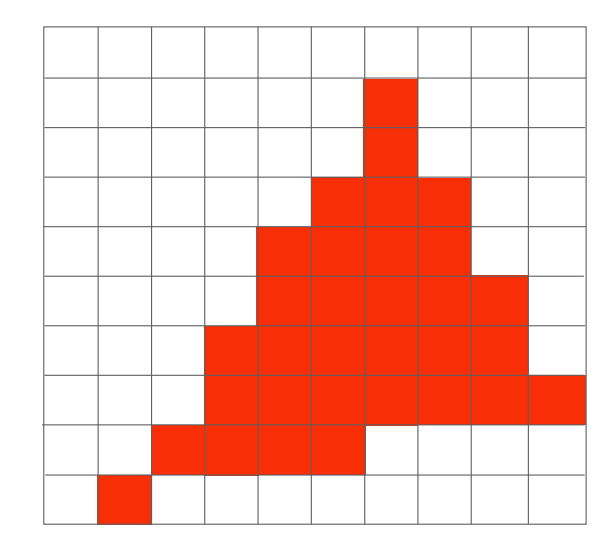
此時你會發現由於每個像素只能是一個均勻的顏色,因此輸出的三角形與原先的會有顯著的差異,雖然形狀基本一致,但會有鋸齒,這個鋸齒就是光柵化圖學裡面一直在致力解決的一個問題
鋸齒產生的原因是因為像素本身有自己一定的大小,導致我們取樣的取樣率對於訊號來說是不夠高的,此時就會產生訊號混疊的問題,反映在這裡就是所謂的鋸齒
因此我們的下一步就是要做抗鋸齒,在訊號與系統裡面被稱為抗混疊
Speed up
這邊最後補充個小插曲,上面的方法需要遍歷所有的像素,我們可以稍微做一些加速,例如紀錄三角形最小與最大的
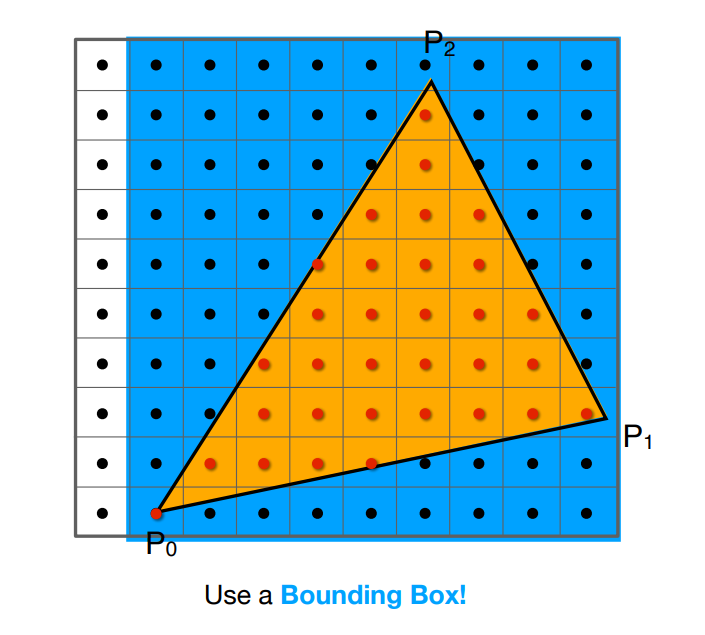
不過這個在三角形是窄長形狀,且又剛好旋轉 45 度分布在包圍盒對角線時,還是會有許多無效區域
另外其實還有很多神奇的加速方法,例如可以針對三角形的每一行都找到最左與最右的位置,並只在該區域中進行判斷,這也類似包圍盒的概念:
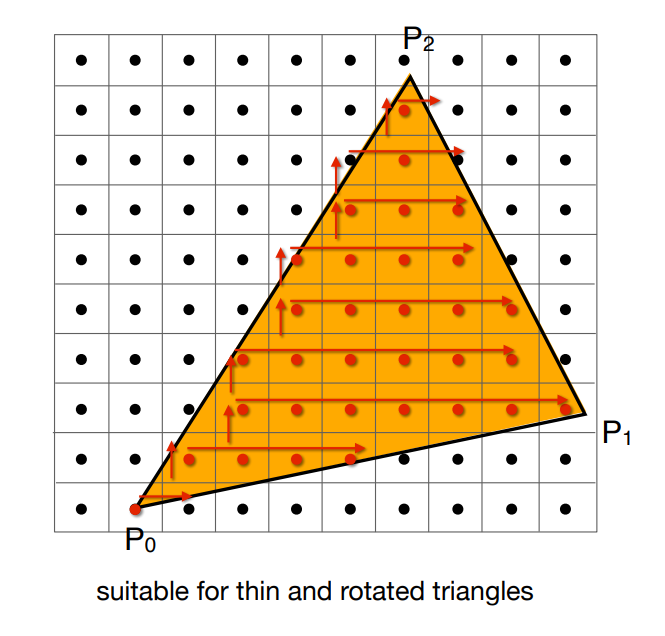
不過這個說起來容易,做起來其實挺困難的
Antialiasing (抗鋸齒)
上面提到鋸齒是因為取樣率對於訊號來說是不夠高,進而產生訊號混疊的問題,這邊可以再看另一個例子 ── 摩爾紋:

右邊那幅圖就是所謂的摩爾紋,它是由左邊這幅圖,將奇數行與奇數列全部去掉的結果,因此它是一張變小的圖,你可以很清楚的看到襯衫上的紋理被扭曲了,領帶的格子變成了一條一條的條紋。 這個在日常生活中也可以看到,例如你拿手機去拍螢幕,你也可以在照片中看到一系列扭曲的條紋
這邊上課還多給了一個影片(連結),你可以看到影片中有些條紋像是在逆時針旋轉,但有些又像是在順時針旋轉:

這是因為人眼在時間中的取樣率不足,跟看高速行駛中的汽車輪子會像是在倒轉是一樣的道理,人眼在時間上的取樣跟不上運動的速度
至此為止我們給了三種取樣率不足的例子:
- 鋸齒:對空間進行取樣
- 摩爾紋:對圖像進行欠取樣(Undersampling)
- 車輪的效應:對時間進行取樣
他們的本質都一樣,函數(訊號) 的變化速度太快了,因此取樣的速度跟不上它,在這種情況下取樣會產生混疊,接下來我們就來簡單介紹一下頻率分析,稍微試著解釋一下原理
在這邊我們先給大家看一下結論,要怎麼做抗鋸齒,或說抗混疊。 答案是先做一次模糊,或者你稱其為濾波(filtering) 也可以,看個例子:
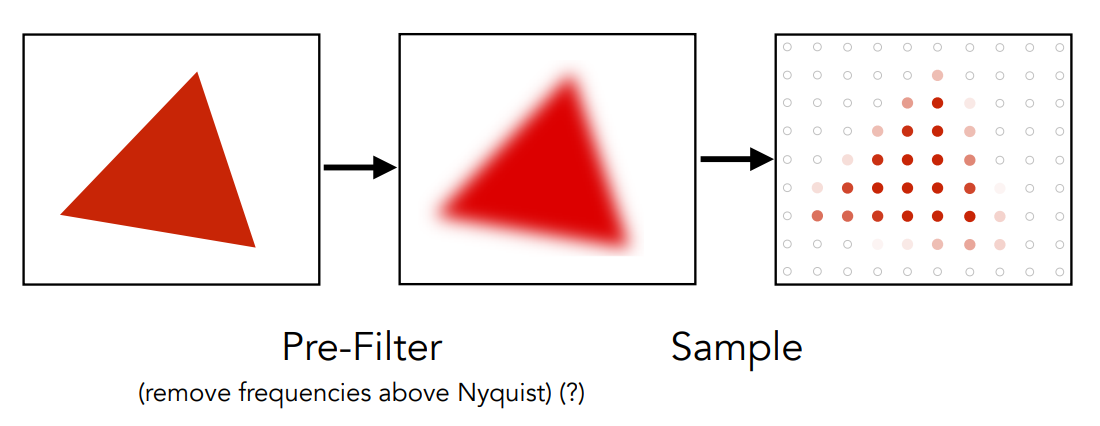
之前的問題在於畫出來的點要麼是紅的要麼是白的,先做一次模糊,再去取樣這個模糊的三角形,就會出現這種有些點是粉紅色的情況,而離中心近一點的點就一樣是紅的
再看個例子,原先的效果:

先模糊再取樣:

要注意是先做模糊再做取樣,再看個例子:

左圖是原圖,可以看見鋸齒現象很嚴重,而右邊是先模糊再取樣的效果
如果改成先取樣再模糊,則會變成下圖左邊的樣子:

這是個對比圖,可以看見右邊的效果遠比左邊好。 左邊這種先取樣再模糊的效果有另一個名字,叫做 blurred aliasing,你可以看到它其實還是有鋸齒,只是被模糊掉了
頻域
接下來就開始來分析它的原理,首先先來解釋什麼是頻域,先從最簡單的東西開始看 ── 正弦波與余弦波:
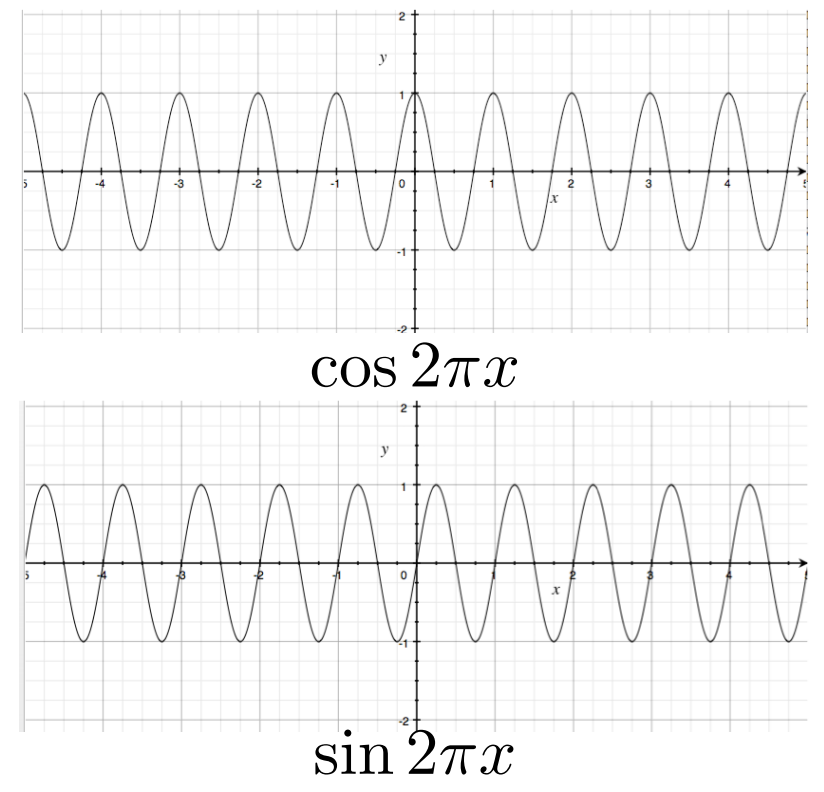
這兩個函數的唯一區別是他們兩個之間相位有一點不一樣,左右平移了一些,那用這兩個波有什麼好處呢?
如果你把正弦和余弦的係數,例如
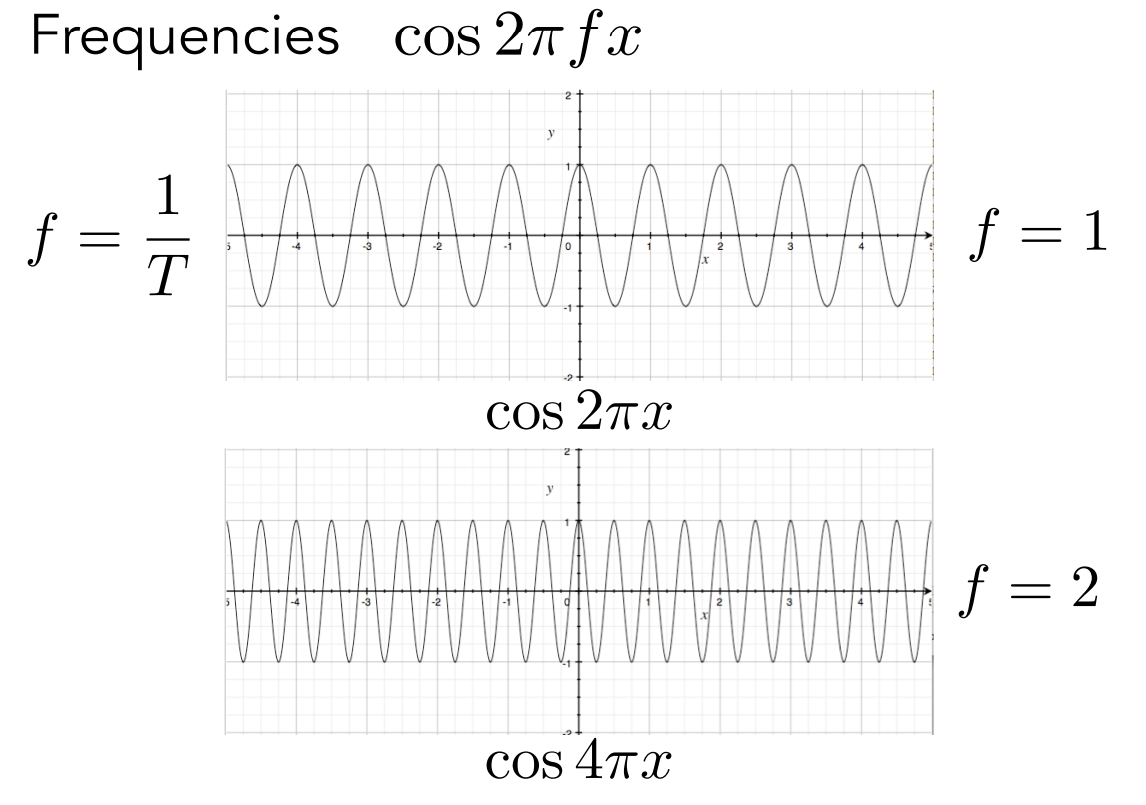
從這裡我們可以再定義一個事情,對於余弦波來說,
通過頻率我們可以分辨出余弦波的變化有多快,例如上圖中很明顯的可以發現頻率為
那為什麼要提到正弦波和余弦波呢? 這邊要回想一下大一微積分裡面提的概念,當中有提到函數的展開,課程裡面會提到各種不同的展開,像是泰勒展開,還有一些其他的展開,但有一個我們會用到的是傅立葉級數展開
傅立葉級數展開說的是任何一個週期性的函數,都可以被寫成一系列正弦和余弦函數的線性組合加上一個常數項:
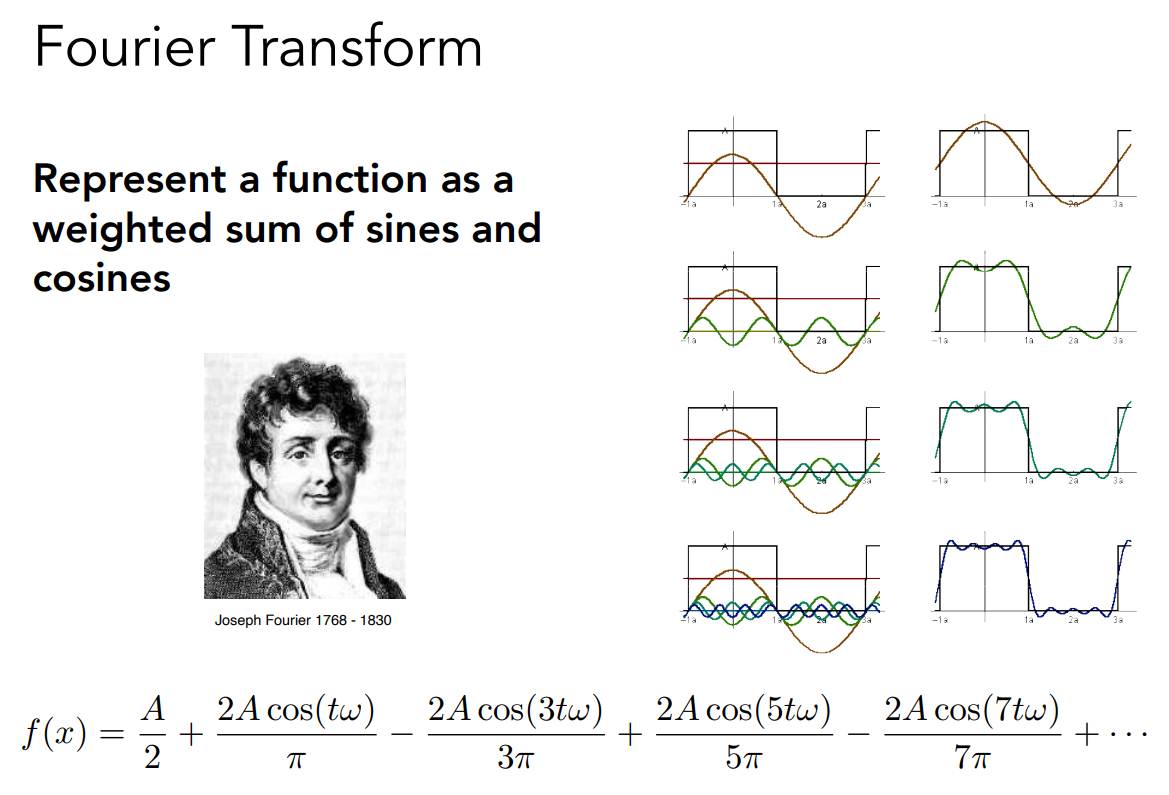
上圖中有一個週期性的方波,可以看見其能被描述為一系列的正弦和余弦函數,當用了更多的項去近似時,其結果也會更接近原先的函數
Info
其中第一項的
傅立葉級數展開與另一個概念 ── 傅立葉變換的關係是緊密相關的,它在講的是給定任何一個函數,都可以讓它經過一個相當複雜的操作,從而轉變成另一個函數:
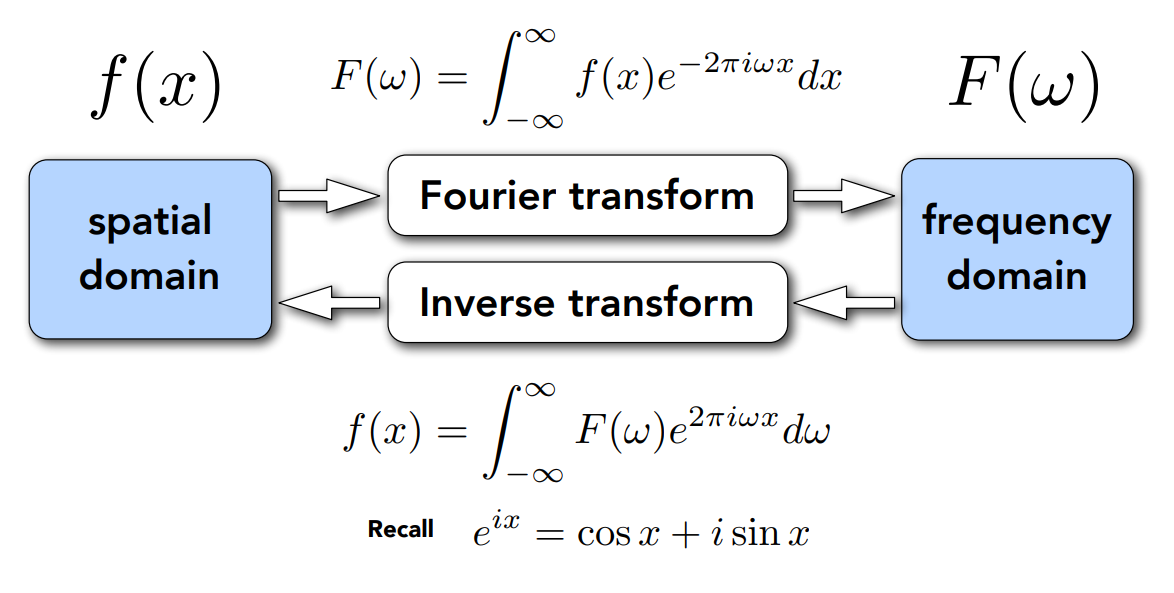
這個複雜的操作我們先不去看它,先注意左邊的
回到正弦波與余弦波,我們剛剛已經知道了他們會有不同的頻率,而傅立葉變換在做的事其實就是把函數,在不同頻率的段落上的值給顯示出來:
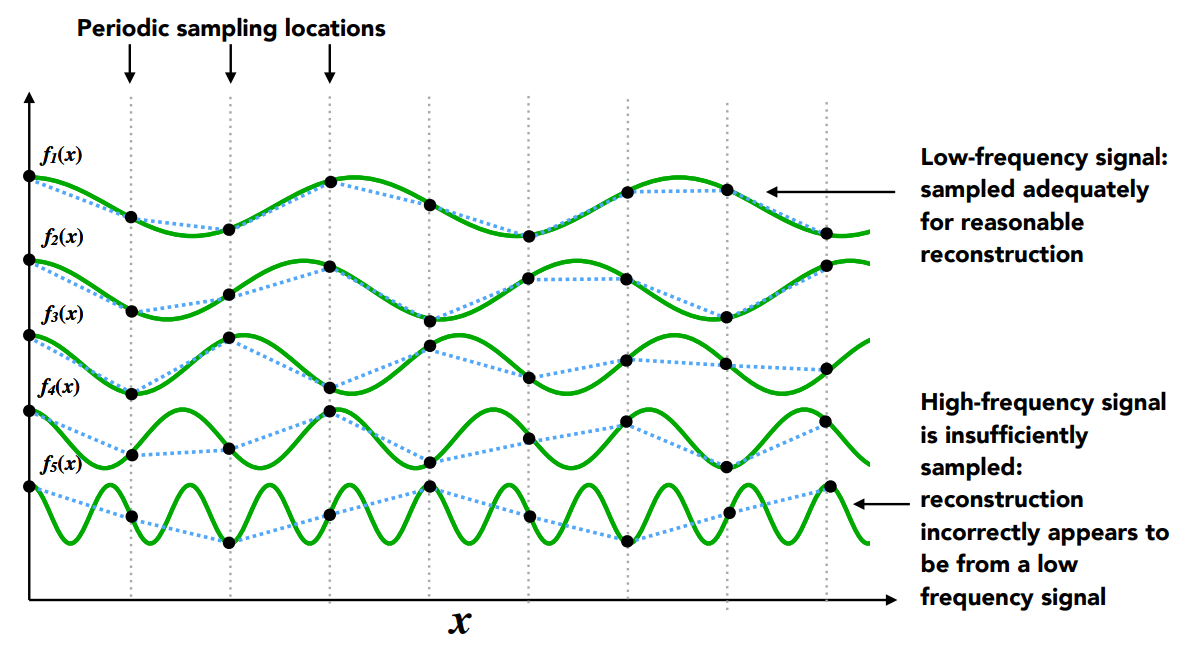
上圖中有五個不同的函數,頻率從低到高為
我們可以發現對於一個函數來說,取樣的頻率能通過上圖的段落間隔反映出來,如果間隔很小,代表取樣的頻率很高,那如果原函數的頻率較高,像是
接著我們再想另一個問題,假設如下圖我們有一個藍色的函數與一個黑色的函數:

這個黑色的函數不是我們恢復出來的函數,單純只是另一個函數。 此時我們以相同的間隔對兩個函數進行取樣,你會發現雖然原函數的頻率截然不同,但我們恢復出來的函數是完全相同的。 以上圖來當例子,無論對藍色函數,還是黑色函數,取樣的結果都是白色空心點
這就是混疊的定義,同一個取樣方法,對兩個不同頻率的函數得到了相同結果,進而導致我們無法區分它們,這就叫混疊
Filtering (濾波/模糊)
那我們現在就來真正分析一些函數,看他們到底擁有什麼樣的頻率,這邊就順便帶一下濾波的概念
從頻率的角度上說,濾波就是把某個特定的頻率給消除掉,前面提的傅立葉變換可以幫助我們理解這個事情,因為傅立葉變換可以將函數從時域變到頻域
直接看例子比較好理解,看下面這張圖:

左邊這幅圖是一個人,不管是什麼樣的圖像,我們都可以利用傅立葉變換將其把圖像從時域轉到頻域,雖然圖像本身不代表任何時間的信息,但我們認為空間上的不同位置也算是時域,這只是它的一個名字。 總之,我們可以把圖像的空間轉換成頻域的空間,也就是右圖
對於右圖,我們把其中心定義為最低頻的區域,周圍則是高頻的區域,也就是說從中心到周圍,頻率會越來越高。 我們使用亮度來表示有多少信息分布在不同頻域的位置上,例如看右圖的頻率,你會發現大部分的信息都是集中在低頻的訊號,因為中間比較亮,對於高頻訊號,不是沒有,但比低頻訊號少太多了,事實上對於自然的圖片來說分布基本上都是長這樣的,這種頻域的圖我們將其稱為頻譜
Info
你可能會發現有兩條水平和豎直的線特別明顯,這是因為在分析一個訊號的時候,我們會將其當作一個周期性重複的訊號,換句話說就是把這張相片無限複製貼上延伸,到了右邊界之後又開始重複左邊的內容,然後繼續往右走,像是這張圖片在水平方向重複了無限次,豎直方向同理
而在正常情況下,很少會有圖像的左邊界和右邊界是完全一致的,因此在圖像的交界處就會產生劇烈的訊號變化,也就是一個極為高頻的訊號,這就是為什麼會有這兩條線
剛才提到濾波可以去掉一些頻率的內容,現在我們可以試著做一下濾波,再將其變換回時域 (照片) 看一下差別,首先是「高通」濾波,把「低」頻的訊號(靠中心) 刪除掉:

我們把低頻訊號都刪掉了,只留下了高頻訊號,此時透過左圖,我們能發現高頻訊號在圖像上代表了輪廓,或說更精確地說法是邊界。 邊界的意義在於其左邊與右邊,或者上面與下面發生了一個突變,差的很多,這時候我們就會認為這是一個邊界,像是圖中的衣服輪廓,或是人物與背景的分界,都發生了劇烈的變化
Tips
「高」頻能「通」過 ⇒ 低頻被刪除,因此稱為高通濾波
接下來換實驗低通濾波:

此時你會發現我們得到了一張模糊的圖,基本還能看出這是什麼,但大部分的細節,像是衣服上的皺褶之類的,我們就看不見了。 從另一個角度來說,高頻代表邊界,因此我們將高頻訊號去掉後邊界自然就變得很模糊了
如果我們同時去掉低頻訊號與高頻訊號,留下了中間某一段頻率的訊號,那就會得到一些不是那麼明顯的邊界特徵:

如果再把這個甜甜圈往外推一點,那就會發現其結果更接近邊界:
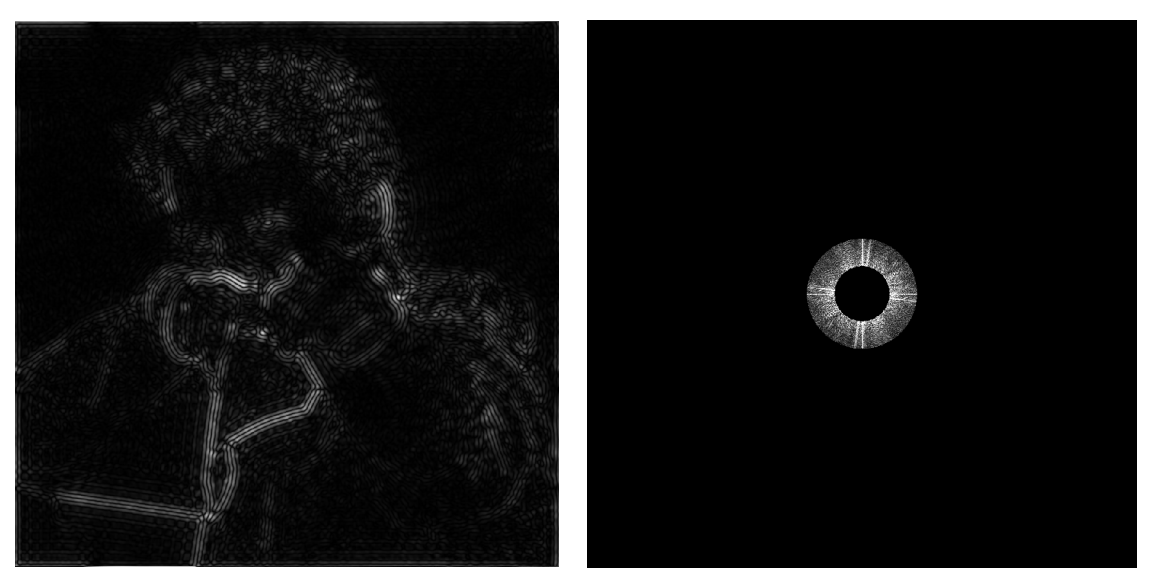
至此,我們就把不同的頻率與訊號的變化聯結在一起了
對於濾波的介紹先到這裡,如果想要學更多可以去修一下數學影像處理,那門課會教不同的濾波方法會產生出怎樣的效果。 另外,現在的影像操作更多是利用機器學習來進行的,頻率方面的操作已經比較少做了,但不管怎麼樣,這個分析的效果還是在的
Convolution (卷積)
介紹完了濾波,也知道了傅立葉變換能給我們怎麼樣的幫助,接下來我們再來細看濾波的過程。 我們剛剛是說濾波可以去掉一段頻率,但還可以從另一個角度上來分析,濾波約等於平均約等於卷積,例如低通濾波器會讓圖片模糊,但模糊本身就是一種平均操作
而卷積在圖學中我們簡化了很多定義,直接用例子來看,比如我們有一個一維的訊號,也就是一個一維陣列,而濾波器(Filter) 就像是一個窗口,可以左右滑動,見下圖:
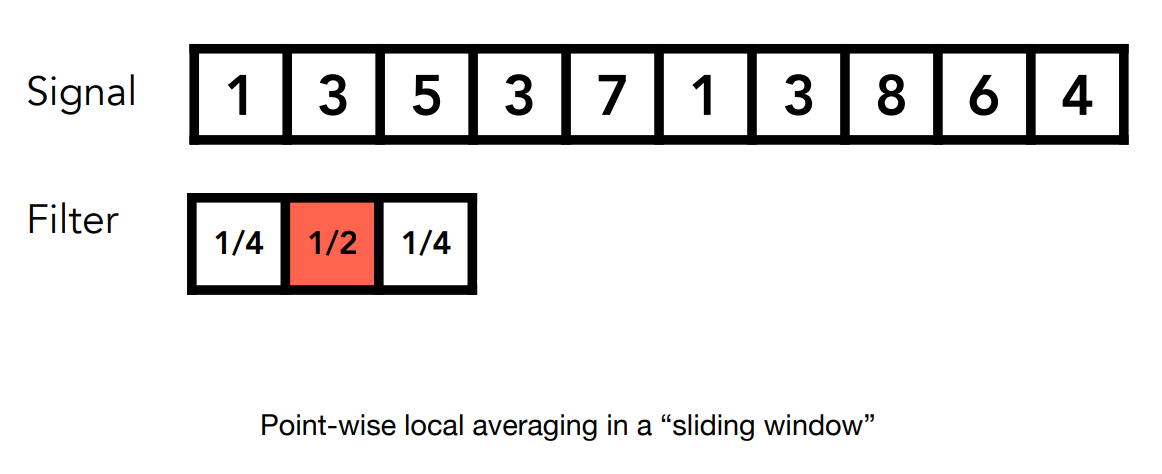
這個窗口的大小有三格,分別有三個數,而卷積操作就是把窗口的三個數,與陣列中對應的三個數做內積,並將結果寫回對應在窗口中心位置的陣列處:
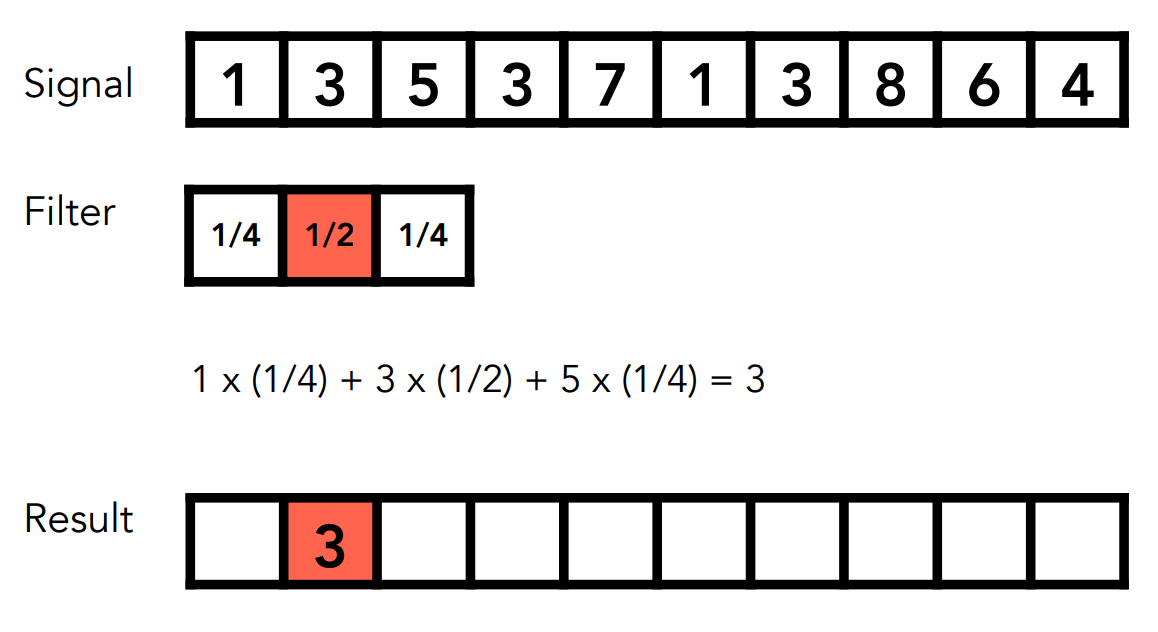
之後移動這個窗口,繼續做一次一樣的運算:
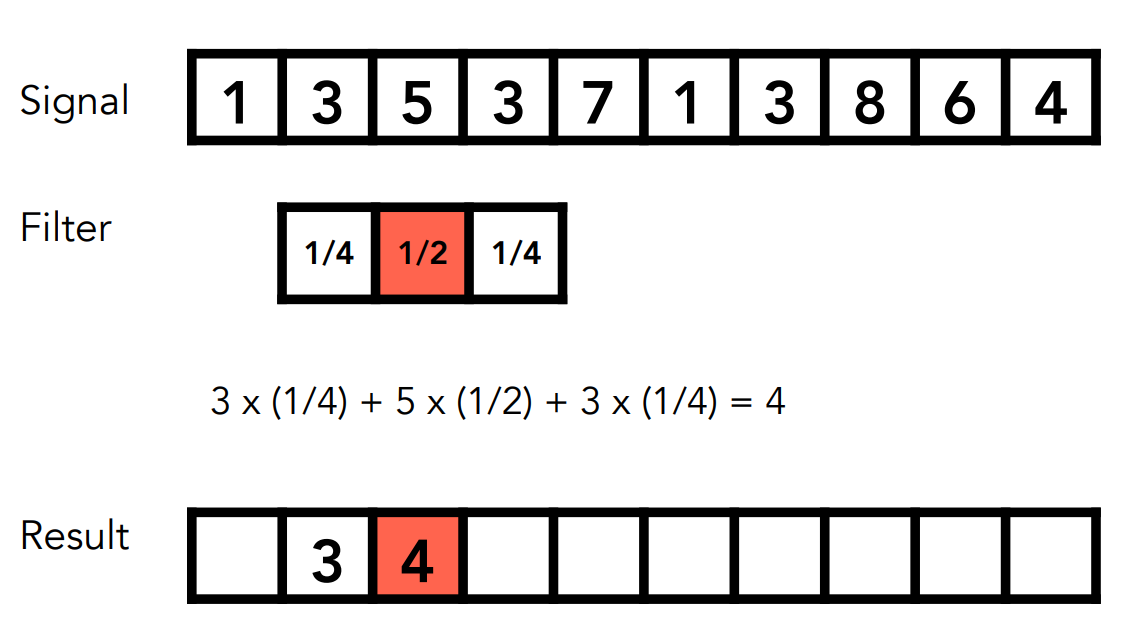
如此重複下去,說白了就是在做加權平均,當然這個定義是圖學中簡化過的定義,而不是數學的嚴謹定義,但這對我們來說就夠用了
而卷積有一個很好用的定理,它的證明比較難,所以這邊只簡單講一下結論 ── 時域上如果我想對兩個訊號進行卷積,那麼它其實對應到兩個訊號在頻域中的乘積
Info
另外,反之亦然,時域上的乘積也可以反過來用頻域上的卷積來操作
因此卷積和乘積這兩個操作其實是挺接近的,通過這個定理,當我們拿到一張圖時,可以直接用某個濾波器去做卷積操作,或是可以把這張圖先傅立葉變換到頻域上,再把濾波器變換到頻域上,然後兩者相乘,最後把結果逆變換回時域上,結果是一樣的:
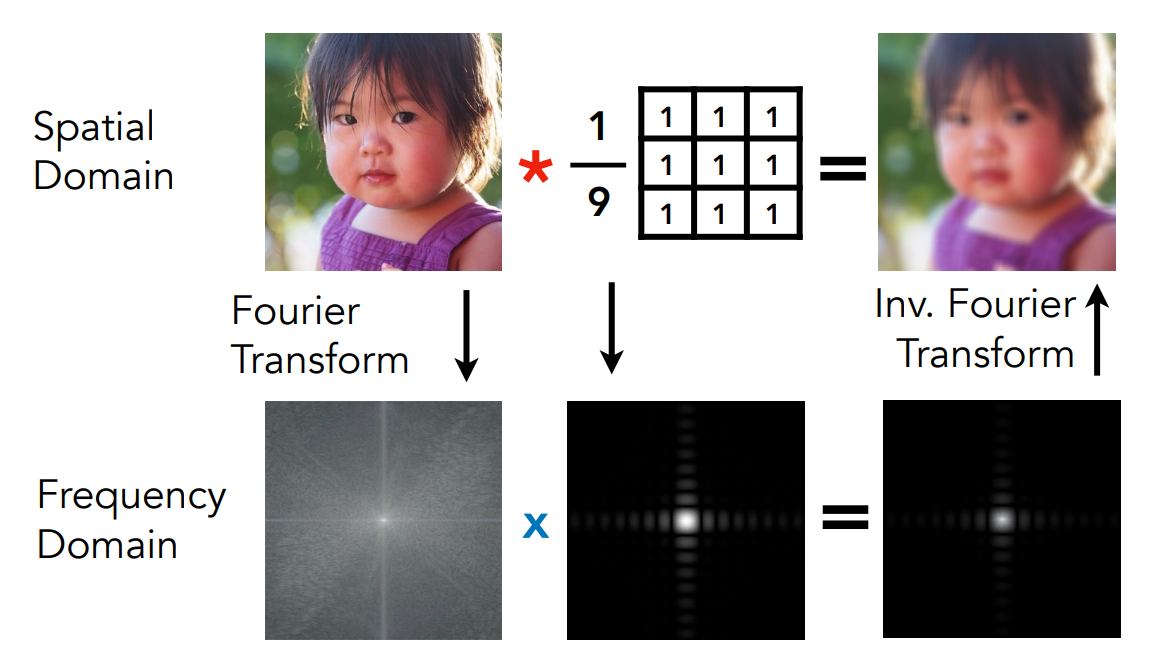
上圖中我們利用一個
而我們也可以先將圖片傅立葉變換到頻域,再將卷積也變換到頻域,接著把兩個訊號乘起來,此時你會發現大部分的地方都變成黑的了,只有中間這塊留下了一些白的部分,將其轉換回時域後就回得到一張模糊過的圖了
從這裡你會發現卷積定理之所以有道理是因為當你把頻率上的兩個訊號乘起來,其效果就相當於在做濾波,以上圖來說就是一個低通濾波,因此圖像自然會變模糊了
Info
上例中除了
這個
Antialiasing (抗混疊/抗鋸齒)
Principle of sampling (取樣的原理)
接下來我們再重新從頻域的角度來看一下什麼是取樣,取樣其實就是在重複頻域上的內容,以下圖為例:
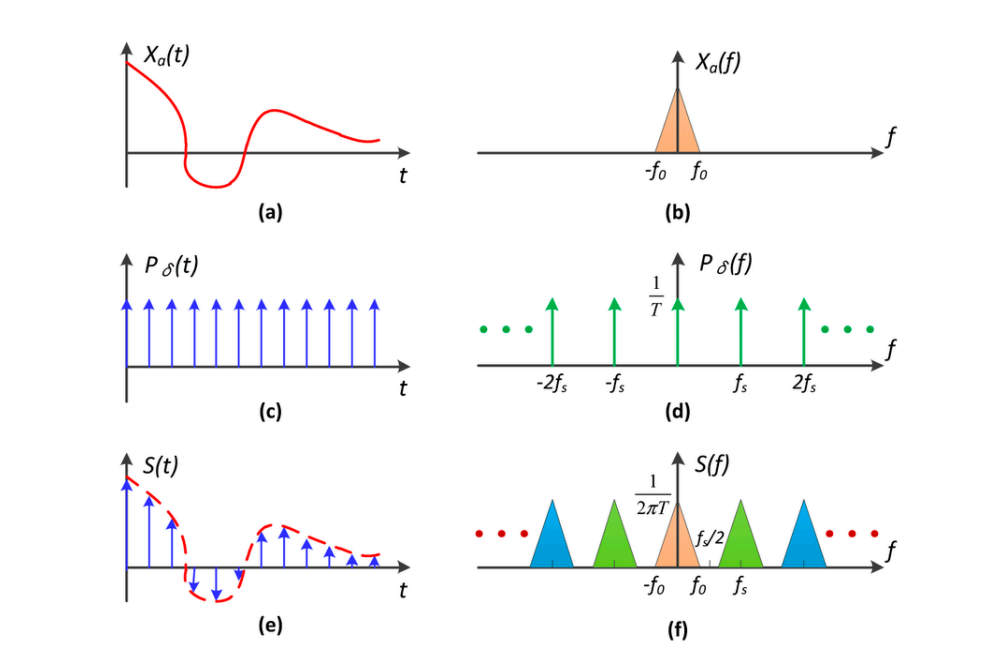
左上角是一個連續函數,假設他在頻域上長右上角那樣 (傅立葉變換的結果),而因為取樣就是要把這些函數變成一系列離散的點,因此我們就留下這個函數在某一些位置上的值就可以了
這就好像我們將兩個函數相乘,以上圖為例,我們拿 (c) 函數與 (a) 函數相乘,得到的就是 (a) 函數上一些離散的點,也就是 (e) 的結果,和我們前面講頻域時那一系列的白色空心點是一樣的道理
Tips
(c) 這一個一個的箭頭是有名字的,叫做脈衝函數 (Impulse response),可以簡單定義為只在這個位置上有值,其他位置上都沒有值
脈衝函數在經過傅立葉變換後會變成另一個脈衝函數,不過間隔會不一樣,間隔的長度為頻率的大小,因此頻率越高,間隔越大
圖中的左邊是在時域上,而前面有提到時域上的乘積可以用頻域上的卷積來操作,也就是說我們要把 (b) 和 (d) 做卷積,其結果為 (f),相當於把原始的函數複製貼上了很多遍
因此,所謂的取樣,就是在重複原始信號的頻譜
Principle of Aliasing (混疊/鋸齒的原理)
到這邊,我們就可以明白為什麼會產生混疊現象了,這是因為取樣的間隔會使目標頻譜以不同間隔來進行複製,那如果我們的取樣率不足,換句話說我們的取樣頻率不夠高,那就會造成傅立葉轉換後其間隔過短,進而導致訊號重疊:
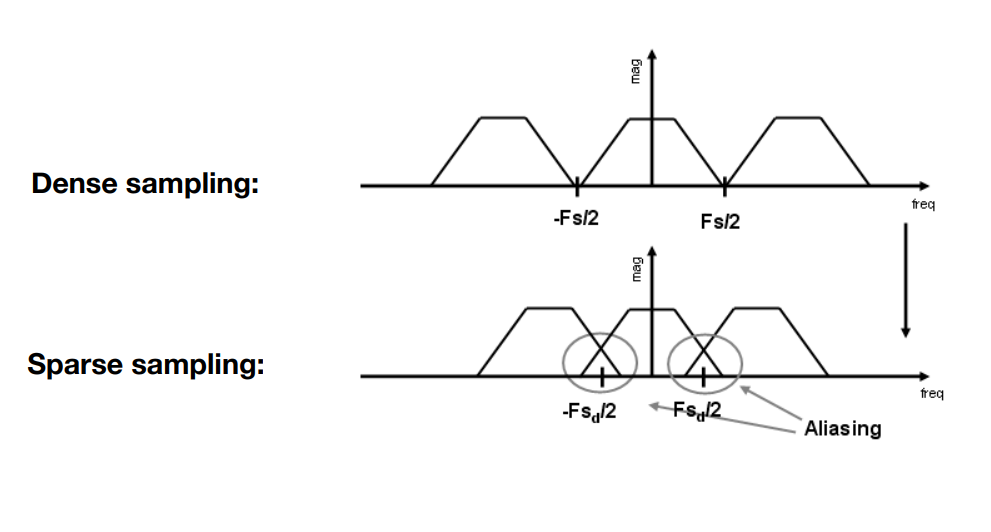
從上圖可以看見訊號產生了重疊,因此造成了訊號混疊,也就是所謂的鋸齒
回到我們最一開始的三角形中,假設三角形下覆蓋的像素較為密集,換句話說單個像素的面積較小,就相當於取樣的頻率較高,因此鋸齒的現象就會少很多,如果每個像素較為稀疏,換句話說單個像素的面積較大,則取樣的頻率較低,像素與像素中心的距離較遠,因此鋸齒的現象就很嚴重
Antialiasing (抗混疊/抗鋸齒)
現在我們知道鋸齒是如何產生的了,因此接下來我們要來想如何做抗鋸齒,這可以有很多很多的做法,首先當然是提高取樣率,這是終極解法,假設你的螢幕解析度是 640x480 的,那它單個像素自然就很大一顆,此時鋸齒自然就很嚴重,如果用了一個超猛的 8K,像是姫宮華恋,那代表在複製頻譜的時候自然就不容易產生混疊的現象。 但這並不是抗鋸齒要做的事情,因為在同一塊螢幕上,解析度的上限就擺在那,受限於物理限制,自然沒辦法這麼做
回到最一開始,我們有先講過結論 ── 先做模糊,再做取樣
通過我們前面這麼長的鋪墊,我們可以知道這是有意義的,所謂的模糊就是低通濾波,也就是把高頻訊號先拿掉,這樣容易產生重疊的區域就被刪去了。 此時再進行取樣,也就是複製貼上,就可以達到在頻域中消去重疊的效果了:
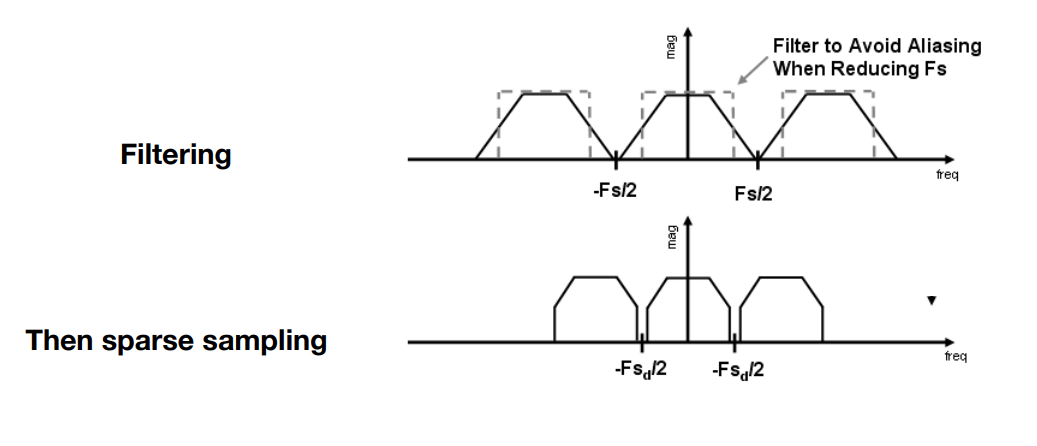
至於模糊要怎麼做,其實利用一個一定大小的低通濾波器,對它進行卷積就可以了。 回到三角形的例子,對於每個像素,其都可能被三角形完全覆蓋,或者完全不覆蓋,又或者部分覆蓋。 我們針對覆蓋的面積進行卷積,就可以把像素的值進行加權平均了:
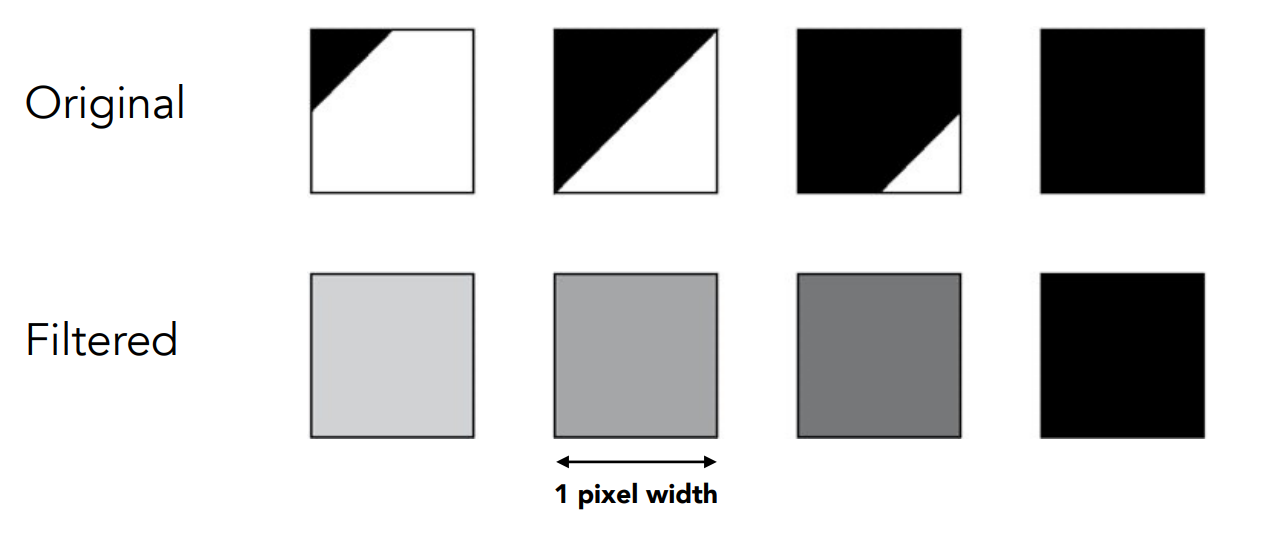
但這件事情說起來容易,真得下去做你卻會發現有點難做,因為我們需要把某一個像素內三角形覆蓋區域的面積算出來,這不容易,而且計算量很大
Multisample anti-aliasing (MSAA)
為了達到計算覆蓋面積的目的,人們研究出來了一種「近似方法」,叫做 Multisample anti-aliasing,簡稱 MSAA,但它僅是一種近似,不能嚴格意義上解決反鋸齒的問題
它的原理是對於每一個像素,我們都在當中新增更多的取樣點,相當於將一個像素再劃分為更多的小像素,這又被稱為超取樣 (Supersampling)
下圖中我們把像素多切了 16 個取樣點出來:
切好取樣點後,我們再接著判斷這些點是不是在三角形內,最後將這個判斷的結果平均起來,作為單個像素的結果,這樣就可以達到對單個像素覆蓋區域的近似效果
我們來實際看個例子,假設我們想對底下這個三角形做抗鋸齒:
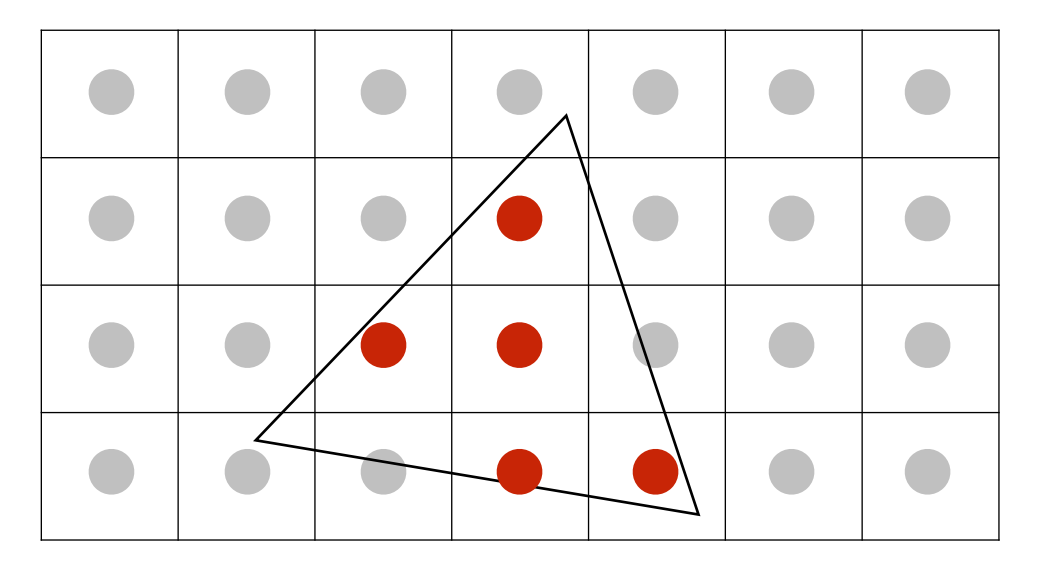
我們可以將其切為 2x2 個區域,也就是 4 個取樣點:
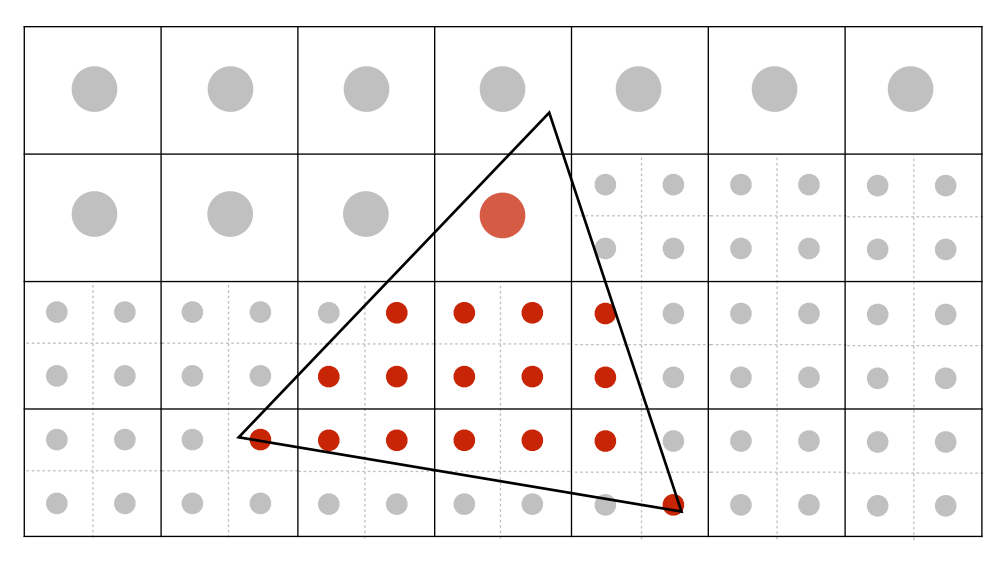
接著逐個判斷取樣點是否有被三角形覆蓋,如果都沒被覆蓋就是 0,一個點被覆蓋則為 0.25,依此類推:
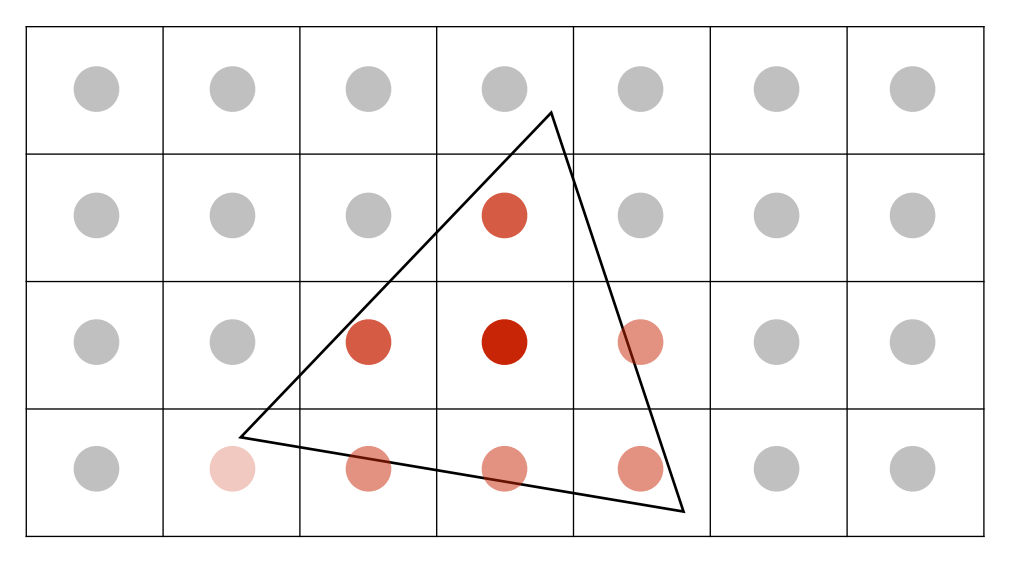
得到所有的近似結果後,再根據其覆蓋比例去調整顏色的強度,例如覆蓋率為 25% 的話就用 25% 的紅色:
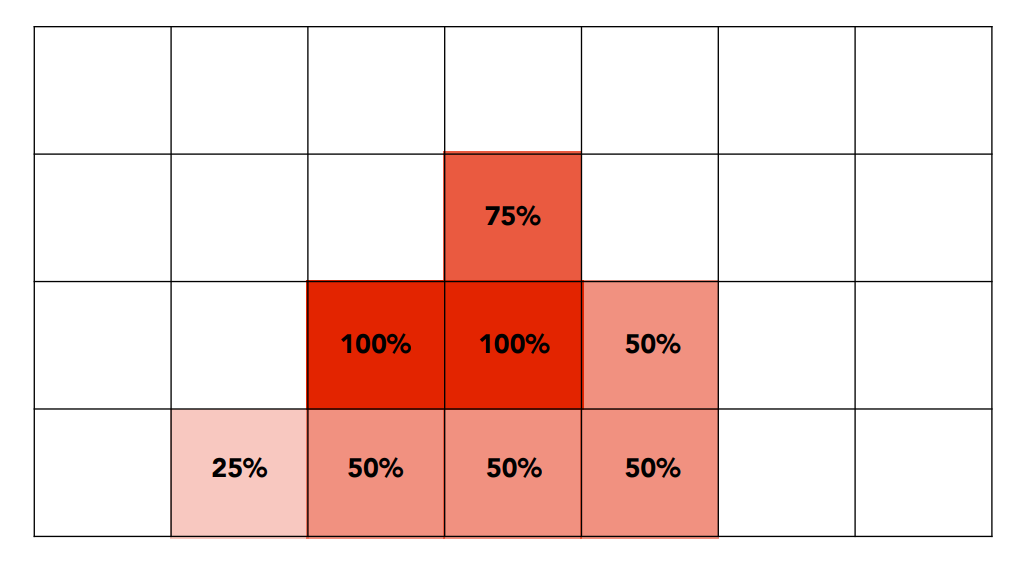
這相當於是我們用一系列的 box 去模糊了這個三角形,做完後要取樣就很簡單了,因為每個格子都是同一個顏色,因此得出來的結果與 MSAA 做完的結果基本一樣,因此取樣的操作相當於是隱含在 MSAA 的過程內了
這邊要提一點是 MSAA 解決的是計算像素內三角形的覆蓋率,也就是解決了「信號模糊的計算」,是一種計算模糊的方法,而不是透過提高解析度解決了鋸齒問題
再來看一下實際的效果
原圖:

MSAA 的結果:

可以看見上圖效果還不錯,但為了引入 MSAA,計算量會成倍數成長,假設使用 4x4 的 Supersampling,則單個像素的計算量就會變 16 倍,因此在工業界的應用上人們通常並不是將單個像素規則的劃分成像 4x4 這樣的區域,而是會用更加有效的一些分布來布置這些取樣點,另外,有一些取樣點還會被鄰近的不同像素所使用
這也是為什麼當大家在打遊戲時,如果開啟了 MSAA,假設用個 2x2 倍,幀率並不會真的變成原來的四分之一
SSAA
另外還有個東西叫 SSAA,他與 MSAA 非常像,應該說 MSAA 是在 SSAA 的基礎上研發出來的。 兩者都會將一個像素再往下分更多取樣點,差別在於 SSAA 的每個取樣點都會執行一次 Fragment Shader code,但 MSAA 的每個取樣點只會計算 Sampling(判斷是否有被三角形覆蓋等),之後再於中心點執行一次 Fragment Shader code
簡單來說,假設以 2x2 的 SuperSampling 為例,SSAA 會生成一個 4 倍大的 frame buffer 與 z-buffer,但 MSAA 只會生成一個 4 倍大的 z-buffer
上例中因為三角形的顏色都相同,所以感受不太出來差別,等到讀完 Shading 部分再回來看應該會懂一些
以下節錄自文刀秋二的回答:
最直接的抗鋸齒方法就是 SSAA(Super Sampling AA)。 拿 4xSSAA 舉例子,假設最終螢幕輸出的解析度是 800x600, 4xSSAA 就會先渲染到一個解析度 1600x1200 的 buffer 上,然後再直接把這個放大 4 倍的 buffer 下取樣致 800x600。 這種做法在數學上是最完美的抗鋸齒,但劣勢也很明顯,光柵化和著色的計算負荷都比原來多了4倍,render target 的大小也漲了 4 倍
MSAA(Multi-Sampling AA)則很聰明的只是在光柵化階段,判斷一個三角形是否被像素覆蓋的時候會計算多個覆蓋樣本(Coverage sample),但是在 pixel shader 著色階段計算像素顏色的時候每個像素還是只計算一次。 例如下圖是 4xMSAA,三角形只涵蓋了 4 個 coverage sample 中的 2 個:
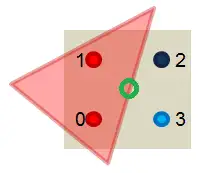
所以這個三角形需要產生一個 fragment 在 pixel shader 裡著色,只不過生成的 fragment 還是在像素中央(位置,法向量等資訊插值到像素中央),然後只運行一次 pixel shader,最後得到的結果在 resolve 階段會乘以 0.5,因為這個三角形只 cover 了一半的 sample
現代所有 GPU 都在硬體上實作了這個演算法,而且在 shading 的運算量遠大於光柵化的今天,這個方法遠比 SSAA 快很多。 順便提一下之前 NV 的 CSAA,它就是更進一步的把 coverage sample 和 depth,stencil test 分開了
Info
原文連結:請問FXAA、FSAA與MSAA有什麼不同?效果和性能上哪個好?
這句「而且在 shading 的運算量遠大於光柵化的今天」原作者說打反了,但我沒看懂是哪裡反了,大家自己注意一下吧,如果搞懂了也拜託告訴我XD
其他相關
這邊再多簡單提兩個現代常用的抗鋸齒方法,除了 MSAA,較為重要的兩種為 FXAA 與 TAA,這兩個得到了工業界的廣泛應用
FXAA
FXAA 是 Fast Approximate Anti-Aliasing 的縮寫,其與增加取樣點沒有任何關係,它的概念是對圖像進行後期處理,也就是說其會先生出一張有鋸齒的圖,接著再想辦法將鋸齒去掉,我們前面有提到先做取樣再做模糊是不可行的,因此它肯定不是這樣做的,關於這點你也可以從頻域分析的角度去想看看
它的做法很簡單,在得到一張有鋸齒的圖時,它會利用一些圖像匹配的方法將把圖中的邊界都找出來,並且把這些邊界暴力的換成沒有鋸齒的邊界,因此他非常的快,而且效果也不錯
TAA
TAA 是 Temporal Anti-Aliasing 的縮寫,是最近幾年才剛剛興起的方法,也是非常簡單且高效,Temporal 的中文是暫時的、短暫的,從這點你可以簡單的推測出其與時間相關
它的做法是去尋找上一幀的訊息,例如找同一個像素,然後看它在上一幀的時候有沒有在三角形內,並將這個資訊應用進來,假設目前的場景是個靜態的場景,那就非常有用,當然對於運動的物體也是有辦法,這個在後面的章節再來討論
Super resolution
還有一個與抗鋸齒很像的概念是 Super resolution,中文叫做超解析度,它的概念是,假設給你一張 512x512 的圖,你要把它拉大成 1024x1024 的,如果直接拉,那肯定全都是鋸齒,換句話說 1024x1024 這張圖是張高解析度的圖,但我們的取樣率不夠,只有 512x512,我們想要把高解析度的圖給恢復出來
因此和抗鋸齒很像,都是要解決取樣率不足的問題,這邊簡單介紹一種做法較 DLSS,它通過深度學習,用猜的把那些缺失的細節給生出來了,也就可以將原本的圖恢復成高解析度的圖了
牽扯到「猜」,那肯定就會利用到深度學習了
Z-Buffer(Depth buffer)
Painter's Algorithm
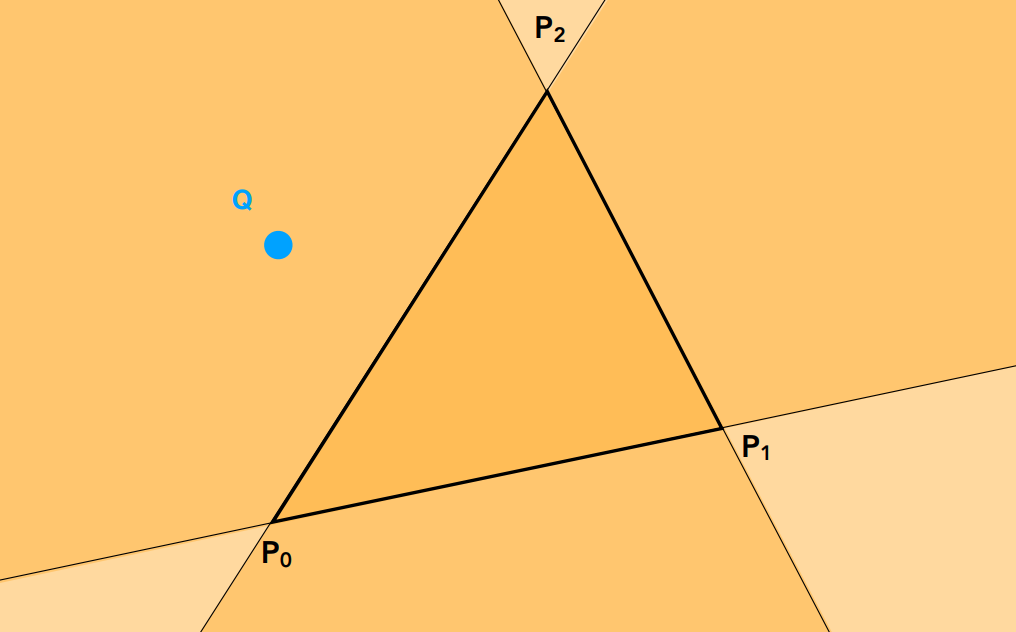
現在回來處理
對於我們來說,就是先對遠處的物體做光柵化,再慢慢往前對近處的物體做光柵化,因為整體流程與畫油畫類似,因此這個方法被稱為畫家演算法(Painter's Algorithm)
假設我們要畫一個立方體,那可以先畫最遠的面,再考慮周圍的四個面,最後再畫上方的面:
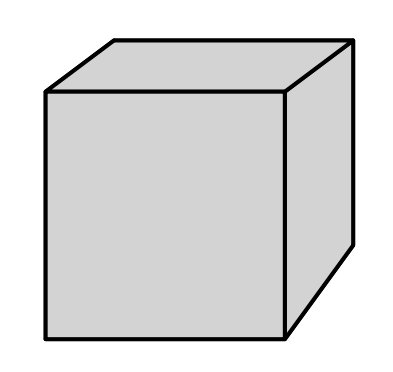
但畫家演算法有一個問題,直接看圖比較好理解:
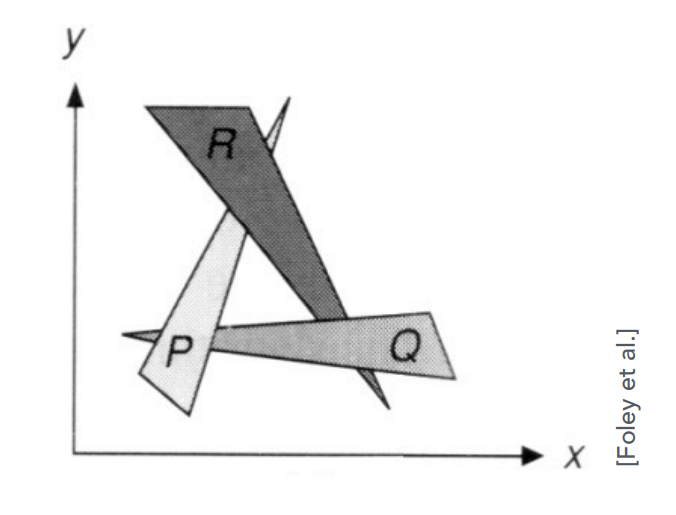
上圖內有三個三角形,P 覆蓋 Q,Q 覆蓋 R,但 R 又覆蓋 P,形成了一個環,屬於一個互相遮擋的關係。 在這種情況下,我們就沒有辦法定義它們的深度關係了,因此也就無法使用畫家算法了
Z-Buffer(Depth buffer)
為此,圖形學引入了一個概念,叫做 Z-Buffer,這是一個目前廣泛採用的演算法,它的想法也很簡單,剛剛的問題是我們判斷的依據是一個物體,現在我們改成針對每個像素來判斷深度關係,紀錄一個像素能見的最淺深度,便可以解決剛剛的問題了
我們通常會在 Rendering 的過程中生成另一張圖,這張圖用來存所有像素紀錄能見的最淺深度,這張圖被稱為深度圖:

上圖的左側為我們 Rendering 的主目標,其為 frame buffer 的結果,而引入 z-buffer 後的副產物就是右圖,用來記錄所有像素對應的深度,並將其反映在顏色上,越近越黑,包括地板的顏色也是
接下來來談如何實作,上一節我們在討論變換的時候提到一個事情:相機放在原點,並看向負 Z 方向。 這邏輯上代表我們看到的所有 Z 值都小於 0,因此數字如果越小,代表離我們越遠,反之數字越大就越近。 由於這個特性,同時為了方便計算,我們還可以將深度可以理解為相機到該像素紀錄的點的距離,距離永遠是正的,而且距離越小越近,與前面的特性相襯
實作上兩種方法都有人用,寫 code 的時候要注意其是如何判斷深度的,下面是一個簡單的範例:
for each triangle T
for each sample (x,y,z) in T
if (z < zbuffer[x,y]) // closest sample so far
framebuffer[x,y] = rgb; // update color
zbuffer[x,y] = z; // update depth
else
; // do nothing, this sample is occluded一樣以上圖為例,假設目標像素一開始先考慮了地板,我們就會把地板的深度給記錄下來,接著來開始考慮立方體,立方體的三角形會告訴我們在目標像素上的深度是多少,然後我們拿這個深度與 Z-Buffer 中紀錄的深度對比,就會發現其深度比較小,此時我們便可以更新 Z-Buffer 了
Info
此例中,一開始 Z-Buffer 的所有元素都會被初始化為無限遠,如此才有辦法紀錄地板的深度
再看另一個例子:
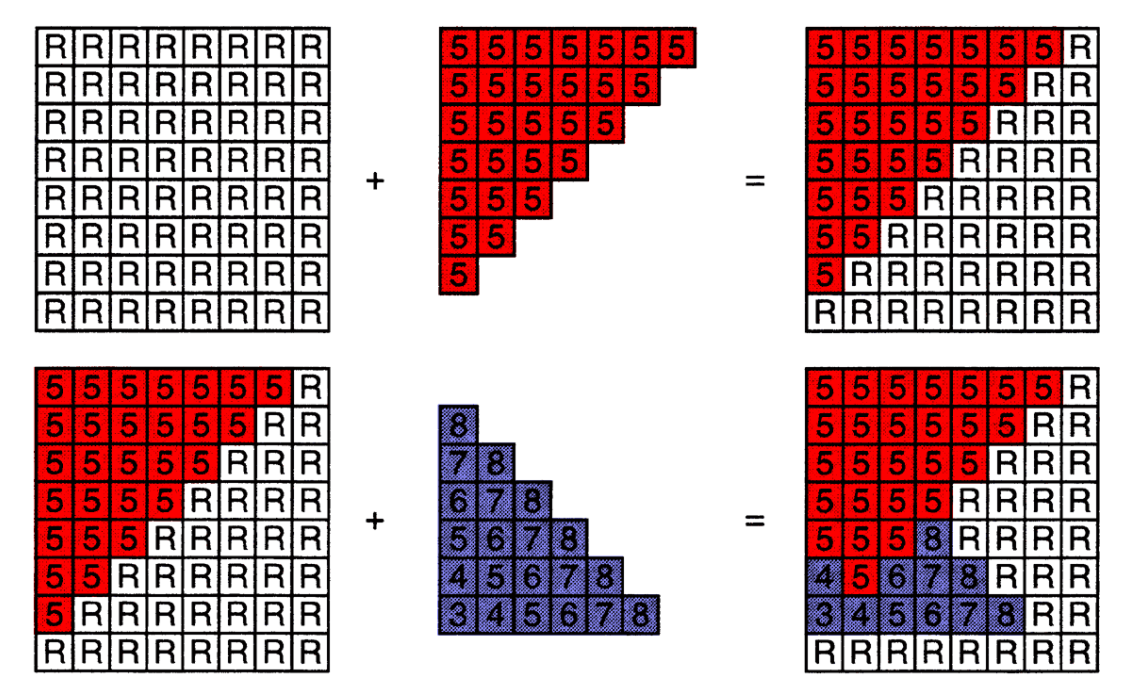
上圖中有兩個三角形,一個紅的一個藍的,紅的三角形深度都為 5,藍色三角形擺的有個角度所以深度各不相同。 我們先判斷了紅色的三角形,因此 Z-Buffer 將紅色三角形的深度更新了進去,接著開始判斷藍色三角形,你可以看到只有深度小於 5 的像素會被更新進去。 如果我們先考慮藍色的三角形,那結果基本上會是一樣的,由此你也可以發現 Z-Buffer 的演算法和順序是沒有關係的,這是一個不錯的特性
你可以發現上圖中兩個三角形互相覆蓋了彼此的一部分,實務上我們通常用浮點數來表示深度,所以很少會出現深度相同的狀況,因此透過維護一張這樣的表,我們就可以得到一個準確的深度關係了
Z-Buffer 的核心思想是以像素為單位來考慮深度,但由於走訪的單位是物體,因此複雜度為
另外,對於 MSAA,如果我們要應用 Z-Buffer,那就還要再考慮其是要以像素為單位,還是以 MSAA 裡面的每個取樣點為單位來建表,通常是會以小的取樣點建表,詳細可見 GAMES101 作業二的 issue(我後來發現他的 code 好像寫錯了XD 不過至少對問題的描述是有幫助的):Games101|作業2 + 光柵化+ SSAA vs MSAA + 黑邊問題
Info
另外,Z-Buffer 處理不了透明物體,透明物體要特殊處理,後面再說
