Games101：MVP Transformation

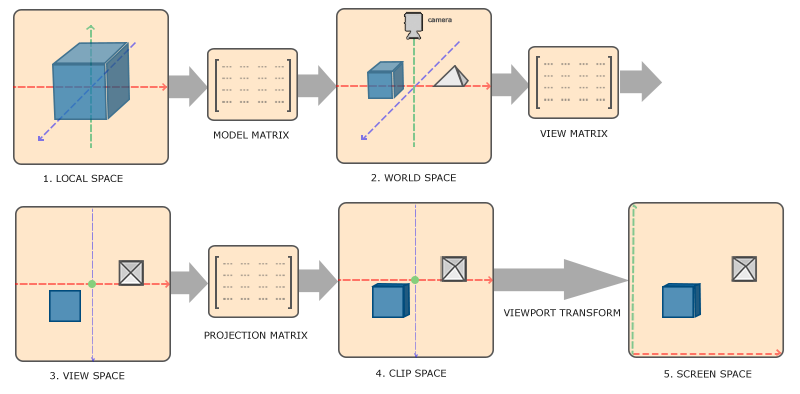
我們的最終目的是將三維的世界顯示在二維的螢幕上，在現實生活中我們可以透過相機拍照來達到這個效果，而在電腦內我們就要試著把這個過程變成一個轉換寫出來

首先我們要決定場景、物品要擺在哪裡，這個我們稱為 model transformation。 這會將物體從自己的座標系轉換到世界座標系（世界空間）中

接下來要找一個好的位置，橋一個好的角度來放相機，這個我們稱為 view transformation。 這會將物體從世界空間轉換到相機空間（camera space），也有人稱之為視圖空間（view space），是以相機為原點的座標系

這兩步完成後我們就可以準備拍照了，所以要將三維的東西投影到二維，這個動作我們稱為 projection transformation。 這會將物體從相機空間轉換到剪裁空間（clip space）中，其會將相機視角外的物體裁剪掉，並保留深度的效果

下面這張是圖來自 Learn OpenGL：

（img src：https://learnopengl.com/Getting-started/Coordinate-Systems）

這三個轉換我們常合起來簡稱為 MVP 轉換。 而前兩個變換通常會一起做，也因此會被合稱為 model-view transformation，接下來我們就來詳細看一下這三個轉換

Model-View Transformation

先來看 model-view transformation，我們的目的是要生出一個以相機為原點的座標系。 首先先講 model transoformation，由於 model transformation 一般來說比較隨意，所以老師也沒多提，這邊補充一下

model transformation 取決於你想把物體放到世界座標系的哪裡，同時套用你要做的旋轉跟伸縮即可，因此你可以用上一章學到的三種矩陣來組合而成，直接給大家看 code 可能比較好理解：

glm::mat4 GameObject::calculateTransformMatrix_() const
{
	glm::mat4 t = glm::mat4(1.0f);

	// Apply transformations in the order: Scale -> Rotate -> Translate
	t = glm::translate(t, position);
	t = glm::rotate(t, glm::radians(rotationDeg.x), glm::vec3(1, 0, 0));
	t = glm::rotate(t, glm::radians(rotationDeg.y), glm::vec3(0, 1, 0));
	t = glm::rotate(t, glm::radians(rotationDeg.z), glm::vec3(0, 0, 1));
	t = glm::scale(t, scale);

	return t;
}

這是我自己引擎裡面更新 model matrix 的函式，基本上就是把 Identity matrix 依序乘上平移、旋轉、伸縮矩陣就可以了。 這裡面的參數串接到了 ImGUI 的介面上，所以在引擎裡面是可以用拉桿之類的元件調整模型位置的

那接下來我們就繼續來看 view transformation，首先思考一下，該如何在電腦裡面擺放一個相機，這需要三個資訊：

• Position $\overrightarrow{e}$
  相機的位置
• Look-at / gaze direction $\hat{g}$
  這個相機面向哪裡，往哪邊看
• Up direction $\hat{t}$
  相機的上下，這很重要，例如閃光燈要裝在相機上方，拿的時候閃光燈要在上面，不能拿反，有時候我們會也會將相機旋轉 45 度之類的。 這個我們稱為 Up direction，用一個向量表示向上方向

如此一來我們就可以把相機給定義下來了，那要這些東西幹嘛呢?

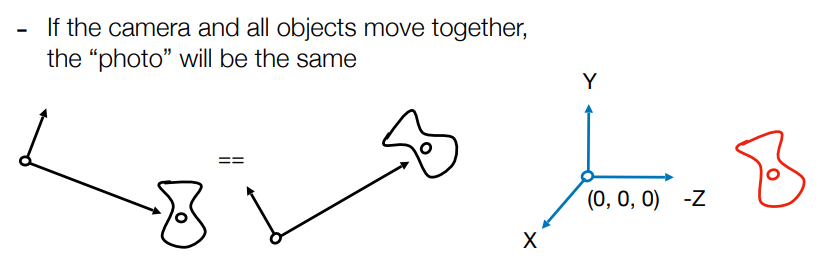
這邊要先提一個問題，在現實生活中當大家坐在車上，如果不往窗戶外面看，是感覺不到自己在移動的，這在物理上稱為相對運動，大家肯定都學過或聽過

那在我們相機的觀察上面也是同一個道理，假如大家是在攝影棚裡拍照，那相同的人與相機，只要相對位置相同，不管實際上在哪個攝影棚拍，拍出來的效果都是一樣的

這個現象可以幫助我們得出一個結果，要達到相機看起來在移動的效果，我們是可以透過改成移動周圍的物體來達到相同目的的，只要保證他們之間沒有相對運動就行，這樣我們就可以讓相機固定在同一位置上了

在習慣上，我們會將相機移動到 $(0,0,0)$ 的位置，看向 $-Z$ 方向，並以 $+Y$ 為向上方向，將世界的座標系轉換為相機的座標系

(這三個相機拍出來的照片會一模一樣)

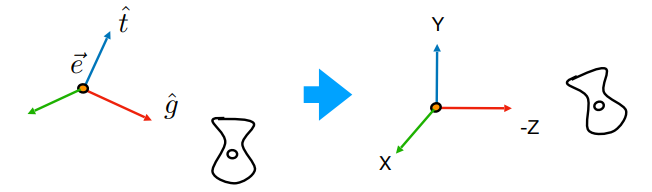
這裡用的是右手坐標系，X 外積 Y 為 Z 方向

那就開始操作看看，繼續沿用前方的符號，假設相機原本是在點 $\overrightarrow{e}$，朝向 $\hat{g}$，向上為 $\hat{t}$，我們現在想要把它放到原點，看向 $-Z$，向上方向為 $Y$，該怎麼做呢?

步驟很簡單：

1. 將相機平移到原點
2. 將 $\hat{g}$ 旋轉到 $-Z$ 方向
3. 將 $\hat{t}$ 旋轉到 $Y$ 方向

這樣做完後自然而然 X 方向也就對上了，這就是我們的基本思路

我們可以將 model-view transformation 的矩陣記為 $M_{view}$，其由一個平移與一個旋轉矩陣構成：

$$M_{view}=R_{view}{T}_{view}$$

對於平移，很簡單的就是將相機原本的位置 $\overrightarrow{e}=(x_e,y_e,z_e)$ 移到原點上：

$$T_{view}=\left[\begin{array}{cccc}1& 0& 0& -x_e\\ 0& 1& 0& -y_e\\ 0& 0& 1& -z_e\\ 0& 0& 0& 1\end{array}\right]$$

重點在旋轉，這裡其實不好寫，你要將任意軸給旋轉到一個規範化的軸上，這個計算很複雜。 但是反過來寫卻很好寫：先將 $-Z$ 軸旋轉到 $\hat{g}$ 方向上，再將 $Y$ 軸旋轉到 $\hat{t}$ 方向，最後再求逆變換就好

所以我們先將 $-Z$ 與 $Y$ 旋轉到對應的方向上，因為是反過來寫的，所以這邊記作 $R_{view}^{-1}$：

$$R_{view}^{-1}=\left[\begin{array}{cccc}{x}_{\hat{g}\times \hat{t}}& x_t& x_{-g}& 0\\ y_{\hat{g}\times \hat{t}}& y_t& y_{-g}& 0\\ z_{\hat{g}\times \hat{t}}& z_t& z_{-g}& 0\\ 0& 0& 0& 1\end{array}\right]$$

隨便拿個方向看一下效果，例如 $-Z$ 方向，注意它第四個元素應當為 $0$，因為是向量：

$$\left[\begin{array}{cccc}{x}_{\hat{g}\times \hat{t}}& x_t& x_{-g}& 0\\ y_{\hat{g}\times \hat{t}}& y_t& y_{-g}& 0\\ z_{\hat{g}\times \hat{t}}& z_t& z_{-g}& 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}0\\ 0\\ -1\\ 0\end{array}\right]=\left[\begin{array}{c}-x_{-g}\\ -y_{-g}\\ -z_{-g}\\ 0\end{array}\right]=\left[\begin{array}{c}{x}_g\\ y_g\\ z_g\\ 0\end{array}\right]$$

的確可以轉到 $\hat{g}$ 方向

如此一來我們就非常輕鬆地將這個矩陣寫出來了，但我們想要的是把 $\hat{g}$ 旋轉到 $-Z$，那要怎麼樣才能得到我們真正想要的矩陣呢?

這時就要再用到一個很重要的性質了，旋轉矩陣是正交矩陣！ 因此

$$R_{view}^{-1}=R_{view}^T$$

換句話說我們只要再將這個矩陣轉置就可以得到我們想要的矩陣了：

$$R_{view}=\left[\begin{array}{cccc}{x}_{\hat{g}\times \hat{t}}& y_{\hat{g}\times \hat{t}}& z_{\hat{g}\times \hat{t}}& 0\\ x_t& y_t& z_t& 0\\ x_{-g}& y_{-g}& z_{-g}& 0\\ 0& 0& 0& 1\end{array}\right]$$

接著只要把它與 model matrix 組合起來就可以了。 至此，我們就成功完成 model-view transformation 了

Projection Transformation

將相機擺好後我們就要將相機面向的東西全部投影到感光元件上，換句話說我們要將面前 3D 的東西全部投影到一個 2D 平面上，這個 3D -> 2D 的轉換就是 Projection Transformation 在做的事情

我們有兩種不同的投影方式：

• Orthographic projection (正交投影 / 平行投影)
• Perspective projection (透视投影)

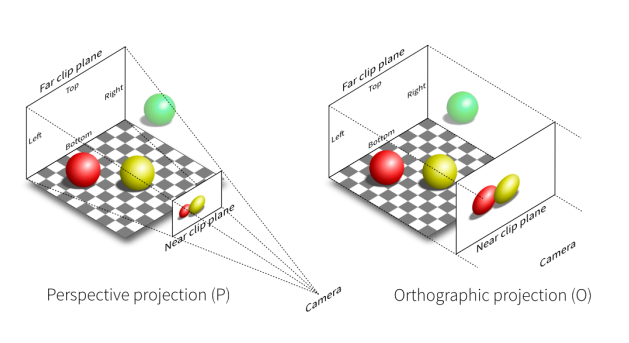
虎書裡面給了一個比較不直觀的例子：

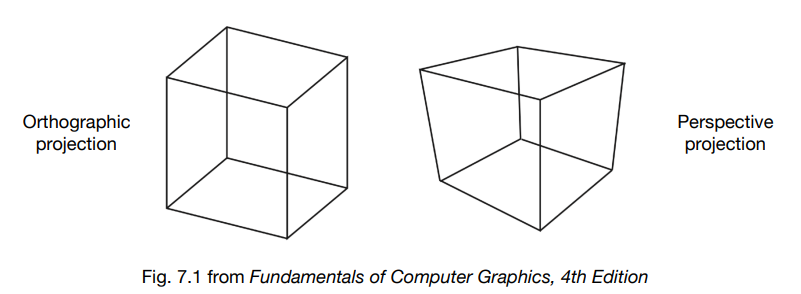
左邊和右邊分別使用了兩種不同的投影方式，你可以看到一個現象，立方體不同的面上有不同組的平行線，一個面由兩組不同的平行線組成

左邊這個立方體的平行線看上去還是平行的，但右邊的立方體就不是了，如果你延長任意一組平行線，你會發現最終它們會相交於某一個點上

如果你學習過素描，或是畫畫，就會知道說右邊的這種投影方式更接近人眼的成像，它會有一個性質：看到的平行線不再平行，最終都會相交到某一個點去，也因此其可以反映近大遠小的特性

(img src: From perspective picture to orthographic picture)

那現在就來看看在數學上要怎麼說這件事情，所謂的透視投影，我們可以認為是把相機放在某一個位置，並近似的將相機認為是一個點，再從這個點連出一個空間中的錐

這是一個四稜錐，在這個四稜錐裡面，我們把近平面到遠平面的區域內的所有東西都顯示出來，並畫在近平面上

而對於正交投影，其實就是假設相機離的無限遠。 以我們上面透視投影的例子來說，將相機拿得越來越遠，近平面與遠平面看起來就會越來越接近，當我們把相機拿到無限遠時，就會發現近平面與遠平面變的一樣大了。 因此在投影出來的結果就會看到，無論物體有多遠，投影到近平面上是不會有近大遠小的效果的

Orthographic projection（正交投影）

那我們就從正交投影開始講，其非常好理解，只要不管遠近，統一將物體擠到某個平面上去就可以了，那這要怎麼做呢?

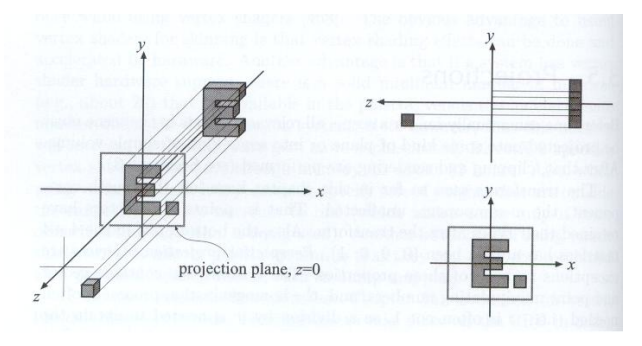
假設相機已被放在了原點，往 $-Z$ 看，向上方向為 $Y$，也許我們僅需要將 Z 座標給扔掉就可以得到正交投影的結果了?

上圖中可以看到有一個三維空間中的字母 E，還有一個小方塊，它們兩個在不同的方向上，如果我們直接把 Z 丟掉，只剩下 X 跟 Y，那得到的結果就是上圖中右下角的結果了。 但這時會有個問題，也就是無法區分物體的前後，因此實際的步驟並不會僅僅是將 Z 丟掉，而是再更複雜一點

此外，我們還需要做個約定俗成的操作：把所有物體都移到 $-1$ 至 $1$ 之間，這可以方便之後的計算。 我們再看個例子，假設空間中有個立方體，如下圖：

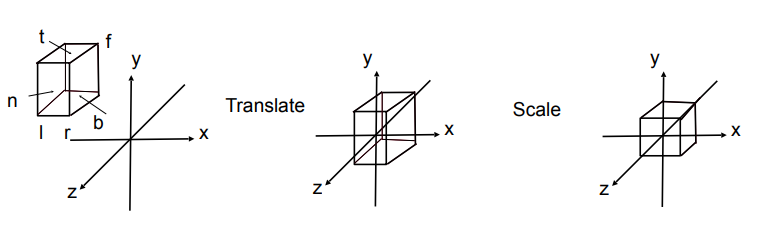
我們只需要定義立方體的左右在 X 軸上是多少，上下在 Y 軸上是多少，遠近在 Z 軸上各占多少的範圍，就可以將這個立方體給描述出來了

我們的目的是將最左方的立方體映射為最右方的標準立方體，英文叫 canonical cube。 可以看到中間多了一個步驟，要先將立方體的中心移到原點，然後把 XYZ 軸都拉伸到 $-1$ 到 $1$ 的範圍就可以了，換句話說就是先做平移再做縮放

Tips

在 X 軸上我們定義左比右小，Y 軸上定義下比上小，但對於 Z 軸的遠近會有點不一樣，仔細看圖中的 Z 是向外的(出螢幕方向)，我們是看向 $-Z$ 方向的，所以如果一個物體離我們較遠，其實代表它的 Z 值較小，較近則 Z 值較大

要注意你用的是哪種座標系，這裡我們用的是右手系所以會有這個問題，如果是左手系，在這點上會比較方便，但左手系的 X 外積 Y 不再等於 Z，因此我們還是偏好右手系

我們現在就來把這個變換寫成數學的形式，用矩陣來做：

$$M_{ortho}=\left[\begin{array}{cccc}\frac{2}{r-l}& 0& 0& 0\\ 0& \frac{2}{t-b}& 0& 0\\ 0& 0& \frac{2}{n-f}& 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}1& 0& 0& -\frac{r+l}{2}\\ 0& 1& 0& -\frac{t+b}{2}\\ 0& 0& 1& -\frac{n+f}{2}\\ 0& 0& 0& 1\end{array}\right]$$

右邊的矩陣將立方體平移到中心，左邊的矩陣則將立方體伸縮為長度為 2 的立方體

Tips

• 立方體的中心為各組頂點相加除以二
• 平移矩陣內填的是負數是因為要將立方體移到原點
• 伸縮為長度為 2 的立方體是因為目標立方體覆蓋各軸的 $-1$ 至 $1$

Perspective projection（透視投影）

理解的正交投影後，透視投影並不難，透視投影是用得最廣泛的一種投影，如前面所說的它滿足近大遠小的性質，帶來平行線不再平行的視覺效果

在說透視投影之前，我們要再回憶一下齊次座標，它有一個定義，向量 $(x,y,z,1)$，表示空間中的點 $(x,y,z)$。 當我將四個數同乘任何一個數 $k$，只要 $k$ 不等於 $0$，那這個 $(kx,ky,kz,k)$ 表示的點就與 $(x,y,z,1)$ 是同一個點。 現在我們更進一步，不要乘 $k$，而是乘以 $z$，此時向量會變成 $(xz,yz,z^2,z)$，仍然是表示空間中的同一個點，等等我們會用到這個性質所以要先有個印象

回到透視投影，它是由一個點開始往外延伸出來的四稜錐所形成的，這個形狀和長方體的差別在於遠平面相對大一點：

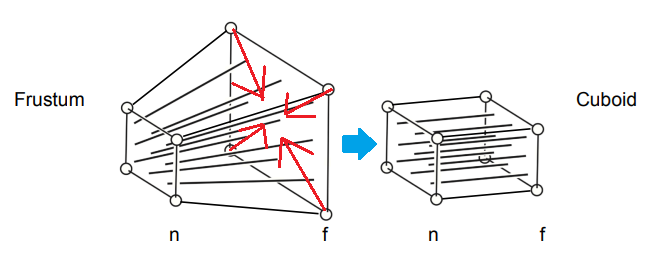
所以我們要做的事情基本上有兩步：

• 把左邊區域中的線拉成右邊的樣子
• 進行正交投影

至於第一步要怎麼拉呢? 我們把遠平面及中間的區域往裡面擠，就可以把四角錐擠成長方體的形狀了，在這個過程中有三點要注意

• 近平面上的點座標不變
• 遠平面上的點 Z 值不變
• 每個平面中心點的 x, y 座標不變

現在就開始擠它，我們從側面來看這個四角錐的話它長這樣(省略下面部分)：

(n 為近平面距離相機的距離，z 為遠平面距離相機的距離)

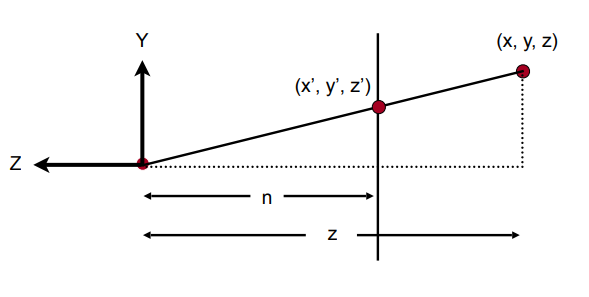
我們想知道對於任何一個點 $(x,y,z)$，經過了擠壓之後座標會如何變化，以上圖來說 $(x,y,z)$ 因為是頂點，因此我們知道他最後的高度與近平面的高度要是一樣的，也就是說 $y$ 經過擠壓後會變為 $y^{\prime }$

再來透過這個側面的視圖，我們可以發現近平面形成的三角形，與遠平面形成的三角形是相似三角形。 因此我們可得

$$y^{\prime }=\frac{n}{z}y$$

按照這個關係，對於任意 Z 值，我們都可以算出對應平面的比值，因此任意一個點的 $y$ 會如何變化是相對簡單的，對於 $x$ 也同理，但對於 $z$ 則不一樣，我們先忽略 $z$ 值，將式子寫出來：

$$y^{\prime }=\frac{n}{z}y{x}^{\prime }=\frac{n}{z}x$$

我們可以將擠壓這個變換以矩陣 $M_{persp\to ortho}$ 表示，並將上式寫為矩陣形式：

$$M_{persp\to ortho}\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]\Rightarrow \left[\begin{array}{c}nx/z\\ ny/z\\ \text{unknown}\\ 1\end{array}\right]==\left[\begin{array}{c}nx\\ ny\\ \text{unknown}\\ z\end{array}\right](\because \text{mult. by z})$$

矩陣內可見 $x$ 經過擠壓後會變為 $nx$，$y$ 同理。 這裡我們透過前面提到的特性，將所有值都乘上了 $z$，以此來消去分母

因此 $M_{persp\to ortho}$ 的形式為：

$$M_{persp\to ortho}=\left[\begin{array}{cccc}n& 0& 0& 0\\ 0& n& 0& 0\\ ?& ?& ?& ?\\ 0& 0& 1& 0\end{array}\right]$$

現在回頭來處理 $z$ 的問題，把不知道的那個 row 填上，根據前面相似三角形的性質，我們只能知道 $x$ 與 $y$ 如何變化，要處理 $z$，需要用到更前面提到的性質：

• 近平面上的點座標不變
• 遠平面上的點 Z 值不變
• 每個平面中心點的 x, y 座標不變

這剛好告訴我們近平面和遠平面上的點 Z 值不會變，因此我們可以將這兩個平面上的點代入剛剛的關係：

$$M_{persp\to ortho}\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]=\left[\begin{array}{c}nx\\ ny\\ \text{unknown}\\ z\end{array}\right]$$

將近平面上的頂點 $(x^{\prime },y^{\prime },z^{\prime })$ 代入，其中因為是在近平面上的點，因此 $z^{\prime }=n$：

$$M_{persp\to ortho}\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ n\\ 1\end{array}\right]=\left[\begin{array}{c}n{x}^{\prime }\\ n{y}^{\prime }\\ n^2\\ n\end{array}\right]$$

這個 $n^2$ 顯然與 $x$ 和 $y$ 都沒有關係，所以我們可以第三個 row 的左邊兩個元素為 $0$：

$$\left[\begin{array}{cccc}0& 0& A& B\end{array}\right]\left[\begin{array}{c}x\\ y\\ n\\ 1\end{array}\right]=n^2$$

也就是

$$An+B=n^2$$

此時我們再將遠平面的中心點 $(0,0,f)$ 代入，同理可得

$$Af+B=f^2$$

Tips

這邊為了避免符號的問題將遠平面的 Z 值由符號 $z$ 改為 $f$

將這個聯立方程式解開後我們可得：

$$\{\begin{array}{l}An+B=n^2\\ Af+B=f^2\end{array}\Rightarrow \{\begin{array}{l}A=n+f\\ B=-nf\end{array}$$

至此，我們便能將這個矩陣填完了：

$$M_{persp\to ortho}=\left[\begin{array}{cccc}n& 0& 0& 0\\ 0& n& 0& 0\\ 0& 0& n+f& -nf\\ 0& 0& 1& 0\end{array}\right]$$

利用這個矩陣，我們就能將透視投影的四角錐擠成一個長方體了，這之後再繼續做正交投影即可

因此，若將透視投影的變換寫為矩陣 $M_{persp}$，則其由正交投影的矩陣與擠壓的矩陣組成：

$$M_{persp}=M_{ortho}{M}_{persp\to ortho}$$

乘出來的結果為：

$$M_{\text{persp}}=\left[\begin{array}{cccc}\frac{2n}{r-l}& 0& -\frac{r+l}{r-l}& 0\\ 0& \frac{2n}{t-b}& -\frac{t+b}{t-b}& 0\\ 0& 0& \frac{n+f}{n-f}& -\frac{2nf}{n-f}\\ 0& 0& 1& 0\end{array}\right]$$

如果是 OpenGL，由於其 NDC 使用左手系，因此長的會不一樣：

$$M_{\text{persp}}=\left[\begin{array}{cccc}\frac{2n}{r-l}& 0& \frac{r+l}{r-l}& 0\\ 0& \frac{2n}{t-b}& \frac{t+b}{t-b}& 0\\ 0& 0& \frac{n+f}{n-f}& \frac{2nf}{n-f}\\ 0& 0& 1& 0\end{array}\right]$$

可以到這邊看更多：https://www.songho.ca/opengl/gl_projectionmatrix.html

FOV of Frustum

這邊補充一下我們如何定義一個四角錐，前面提到立方體可以用 X、Y、Z 軸的覆蓋，也就是六個數字去表示一個立方體

而要定義一個四角錐其實也很簡單，我們從相機出發，看向某一個區域，如果假設我們看到的就是近平面，那麼我們可以給近平面定義一個寬度和高度，就好像人在看螢幕一樣

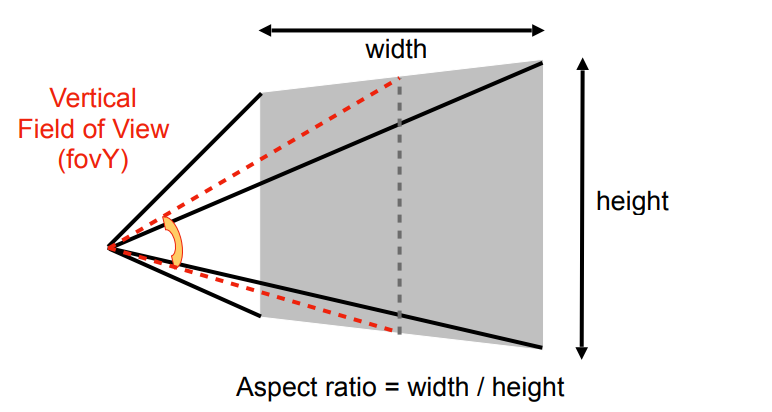
我們可以給螢幕定義一個寬高比，這被稱為 aspect ration，值為寬度除以高度。 另外還有一個概念，如果有玩過相機的可能會知道，叫做視角，英文叫 field of view，表示可以看到的角度範圍

以上圖為例，我們可以在螢幕的中間畫出兩條紅線來，各連到上下兩邊的中心點，而這兩條紅線所夾的角度就被稱為視角

有了這兩個概念我們就可以來定義四角錐了：

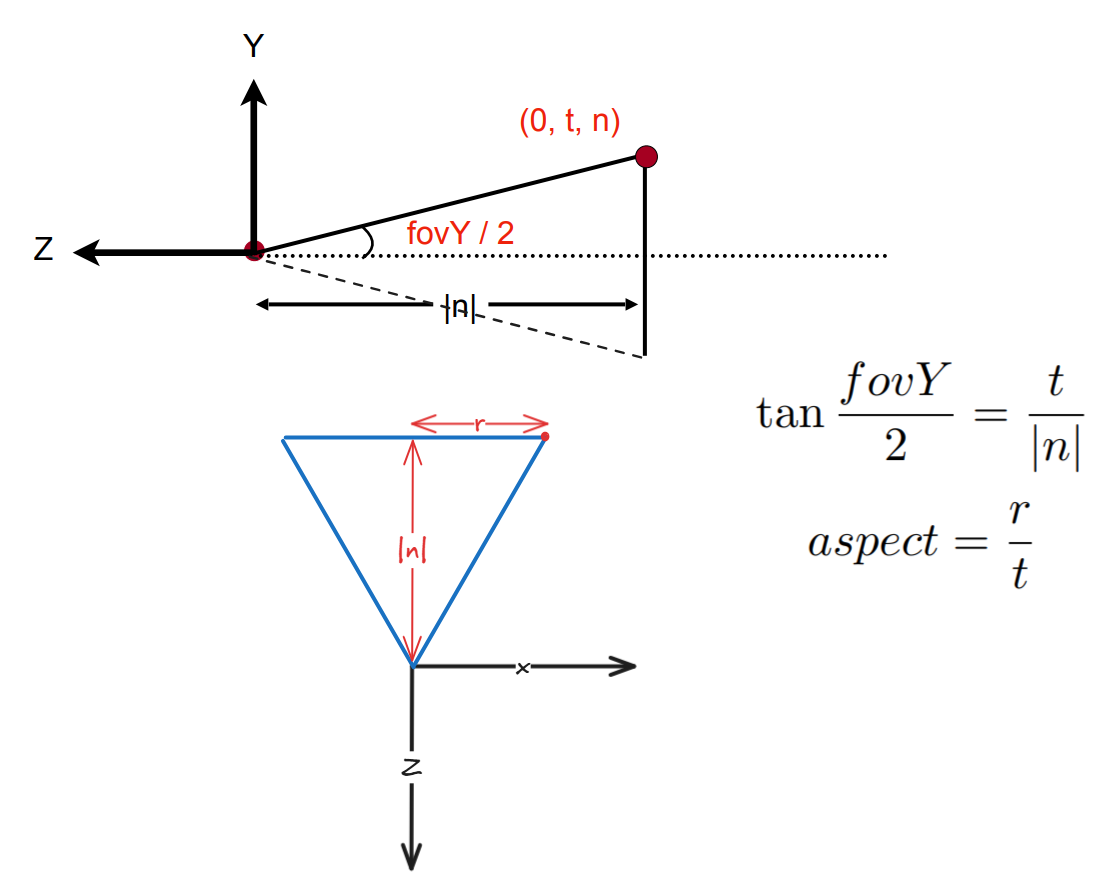
左上角的右邊那條線為近平面，與相機的距離為 $|n|$，而垂直可視角度為 $fovY$，如此一來馬上就可以知道這個三角形的三角函數關係了

Viewport Transformation

到目前為止，MVP 就已經做完了，無論用的是正交投影還是透視投影，此時所有的物體就都已經被擺到了 -1 ~ 1 的立方體裡，下一步我們需要將它畫到螢幕上

因此我們需要先把螢幕的概念定義好，在圖學中螢幕被抽象的認為是一個二維陣列，陣列的每個元素是一個像素，假設你的螢幕是 1920x1080 的，那就表示有這麼多的像素形成了一個二維陣列

換句話說螢幕可以被表示成一個坐標系，這個坐標系我們通常稱其為螢幕空間(screen space)，虎書內有自己的一套坐標定義方式，而這邊(GAMES101) 我們有另一套定義方式：

螢幕的左下角為原點，向右是 $X$，向左是 $Y$，坐標以完整的 $(X,Y)$ 組成，因此圖中藍色像素的坐標為 $(2,1)$，因此整個 $X$ 為 0 ~ width-1，高度為 0 ~ height-1

雖然我們是用整數的坐標來描述它，但你可以很明顯地看到像素的中心，以藍色的像素為例，是 $(2.5,1.5)$，因此對於每個像素，其寬度為 $1$，中心應該要準確地在 $(x+0.5,y+0.5)$ 上

到這邊就可以來表示螢幕空間了，我們現在有一個 -1 ~ 1 的立方體，要把它轉換到 0 ~ width 乘以 0 ~ height 上。 我們知道 -1 ~ 1 的立方體寬度和高度都為 2，因此首先將其除以 2，再乘以對應的 width 和 height，這就是所謂的 Viewport Transformation：

$$M_{viewport}=\left[\begin{array}{cccc}\frac{width}{2}& 0& 0& \frac{width}{2}\\ 0& \frac{height}{2}& 0& \frac{height}{2}\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$

記得這會先做拉伸再做平移

左上角的 $3\times 3$ 矩陣是個對角矩陣，把寬度變成 width，並把高度變成 height，但此時中心還在原點 $(0,0)$，但螢幕空間的左下角才是原點，因此要把中心移到螢幕空間對應的中心上，所以要移動 $\frac{width}{2}$ 與 $\frac{height}{2}$

Tips

你可能會想到一個問題，$Z$ 怎麼辦，立方體是三維的，但螢幕是二維的，這個我們先暫時不管，後面會再提到