Games101：Homogeneous Coordinates(齊次座標)

一般的轉換可以寫成矩陣的形式，像是

$$\{\begin{array}{l}{x}^{\prime }=sx\\ y^{\prime }=sy\end{array}$$

我們可以寫成

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}s& 0\\ 0& s\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$$

因此我們有了 Scale Matrix、Reflection Matrix、Shear Matrix、Rotation Matrix 等等，這些都可以寫成矩陣乘向量的形式：

$$x^{\prime }=Mx$$

或我們說的更精確一點，他們是線性轉換

然而當我們今天做平移的操作時，像是這樣：

$$\{\begin{array}{l}{x}^{\prime }=x+t_x\\ y^{\prime }=y+t_y\end{array}$$

那他就只能寫成：

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]+\left[\begin{array}{c}{t}_x\\ t_y\end{array}\right]$$

而不能寫成上方那種單純的矩陣乘向量的形式了，或者說他不是線性轉換了，變成了一個特例

然而我們並不希望將平移視作一個特殊狀況，畢竟平移蠻常用的，因此就需要使用齊次座標

首先是二維的轉換，在向量上多了一個維度來表示是點還是向量：

• 2D 點 = $(x,y,1{)}^T$
• 2D 向量 = $(x,y,0{)}^T$

注意都是縱向量，這是圖學上的習慣

多了一個維度後平移便可以用矩陣乘向量來表示：

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ w^{\prime }\end{array}\right]=\left[\begin{array}{ccc}1& 0& t_x\\ 0& 1& t_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=\left[\begin{array}{c}x+t_x\\ y+t_y\\ 1\end{array}\right]$$

可以看見原本點 $(x,y,1{)}^T$ 經過平移後仍然是一個點(第三個元素為 $1$)

這邊要提一下，第三個維度是有設計過的，在 $1$ 是點 $0$ 是向量的狀態下，會有下面這些性質：

• 向量 + 向量 = 向量
• 點 - 點 = 向量
• 點 + 向量 = 點
• 點 + 點 = 兩點中點

對於最後一點，人們後來擴充了齊次座標的意義，向量

$$(x,y,w),w\ne 0$$

的實際 xy 座標為

$$(\frac{x}{w},\frac{y}{w})$$

也就是說兩點相加的結果會變為兩點的中點，因為 $w$ 為 2

Affine Transform(仿射轉換)

使用齊次的優點就是可以將這類的轉換：

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]+\left[\begin{array}{c}{t}_x\\ t_y\end{array}\right]$$

直接寫成矩陣乘向量的形式：

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{ccc}a& b& t_x\\ c& d& t_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]$$

這類轉換我們稱其為仿射轉換，使用齊次座標，我們就可以只用一個矩陣來表示仿射轉換了

也可以簡單看幾個二維的線性轉換：

• Scale Transform

  $$S(s_x,s_y)=\left[\begin{array}{ccc}{s}_x& 0& 0\\ 0& s_y& 0\\ 0& 0& 1\end{array}\right]$$

• Rotation Transform

  $$R(\alpha )=\left[\begin{array}{ccc}cos(\alpha )& -sin(\alpha )& 0\\ sin(\alpha )& cos(\alpha )& 0\\ 0& 0& 1\end{array}\right]$$

• Translation Transform

  $$T(t_x,t_y)=\left[\begin{array}{ccc}1& 0& t_x\\ 0& 1& t_y\\ 0& 0& 1\end{array}\right]$$

其中有一點很重要的是 $R(\alpha )$ 是正交矩陣：

$$R_{-\theta }=\left[\begin{array}{ccc}cos\theta & sin\theta & 0\\ -sin\theta & cos\theta & 0\\ 0& 0& 1\end{array}\right]=R_{\theta }^T$$

By definition：

$$R_{-\theta }=R_{\theta }^{-1}$$

Inverse Transform(逆轉換)

如果我們對一個點進行仿射操作後想要讓他回到操作前的樣子，那可以直接將點乘上原先的逆矩陣，舉個例子，將 $(1,1{)}^T$ 平移到 $(3,4{)}^T$：

$$\left[\begin{array}{c}3\\ 4\\ 1\end{array}\right]=\left[\begin{array}{ccc}1& 0& 2\\ 0& 1& 3\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}1\\ 1\\ 1\end{array}\right]=\left[\begin{array}{c}1+2\\ 1+3\\ 1\end{array}\right]$$

若我們想將 $(3,4{)}^T$ 移回 $(1,1{)}^T$，只需要乘上 $M^{-1}$ 就好，先算出 $M^{-1}$

$$M^{-1}=\left[\begin{array}{ccc}1& 0& -2\\ 0& 1& -3\\ 0& 0& 1\end{array}\right]$$

然後乘上去：

$$\left[\begin{array}{c}1\\ 1\\ 1\end{array}\right]=\left[\begin{array}{ccc}1& 0& -2\\ 0& 1& -3\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}3\\ 4\\ 1\end{array}\right]=\left[\begin{array}{c}3-2\\ 4-3\\ 1\end{array}\right]$$

如此一來便可以回到操作前的狀態了

Composition(組合)

我們可以將不同的轉換先依序相乘組合成一個矩陣，這樣跟把轉換矩陣一個一個乘上去的結果會一樣，在寫的時候要注意轉換的順序

舉個例子，將點 $(x,y{)}^T$ 先旋轉 45 度，然後進行一個單位的平移，那可以寫成這樣：

$$T_{(0,1)}\cdot R_{45}\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=\left[\begin{array}{ccc}1& 0& 1\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}cos({45}^{\circ })& -sin({45}^{\circ })& 0\\ sin({45}^{\circ })& cos({45}^{\circ })& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]$$

因為矩陣有結合率，我們可以將其組合，寫成：

$$\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=\left[\begin{array}{ccc}cos({45}^{\circ })& -sin({45}^{\circ })& 1\\ sin({45}^{\circ })& cos({45}^{\circ })& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]$$

這裡有個重點是，當我們把它合成一個矩陣的時候，要記住它是先做線性變換再做平移，如果你要先做平移，就要分開寫成兩個矩陣

舉個簡單的應用範例

假設我們想要將左圖透過轉換變成右圖：

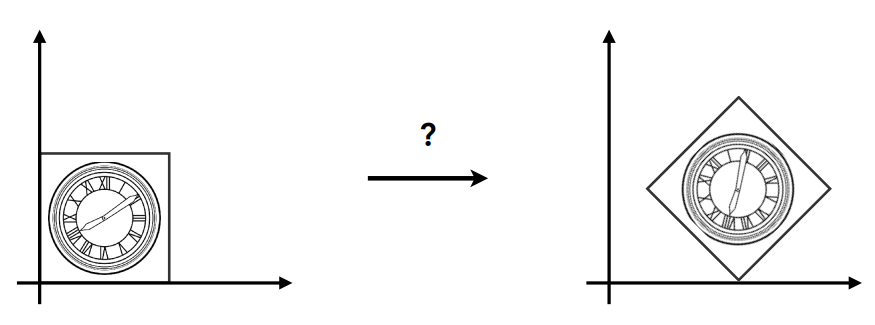
讀完了上面的你，肯定可以知道這可以透過平移與旋轉達成，但是這時候要注意順序。 假設你先是先平移再旋轉，則會變成下圖的樣子：

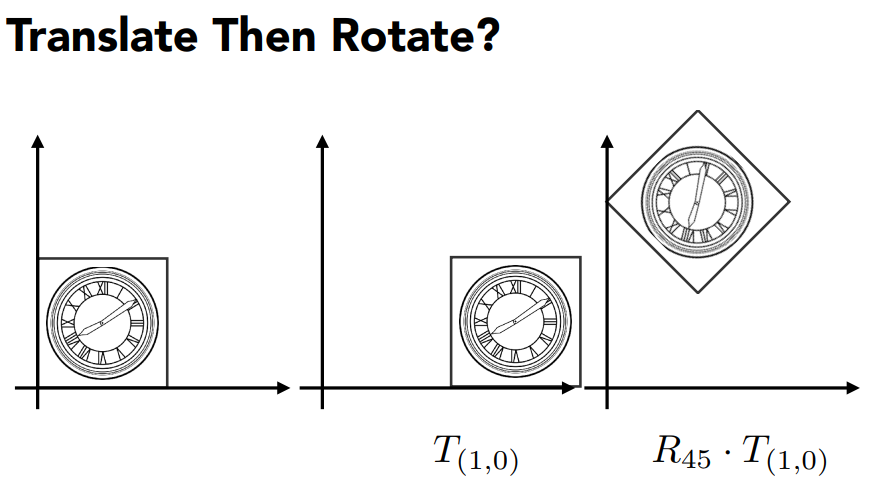
這個例子中我們需要先旋轉再平移：

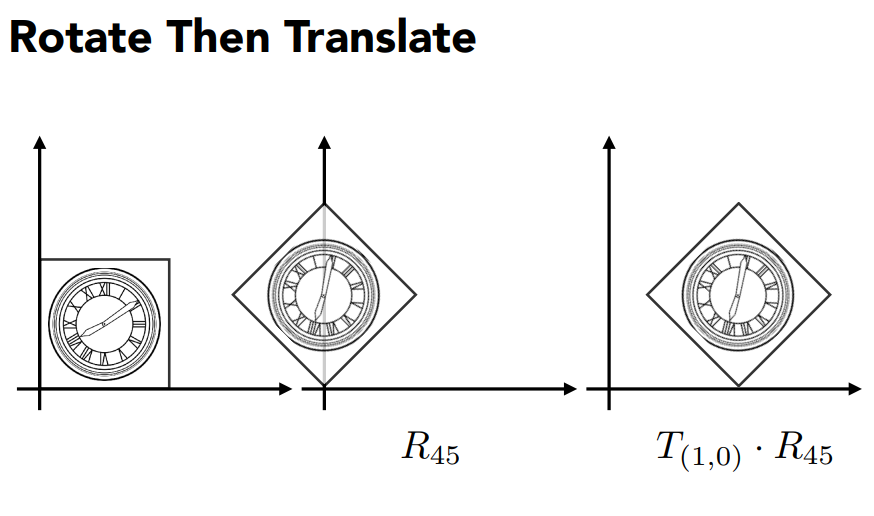
同時這些變換是可以做分解的，看以下例子：

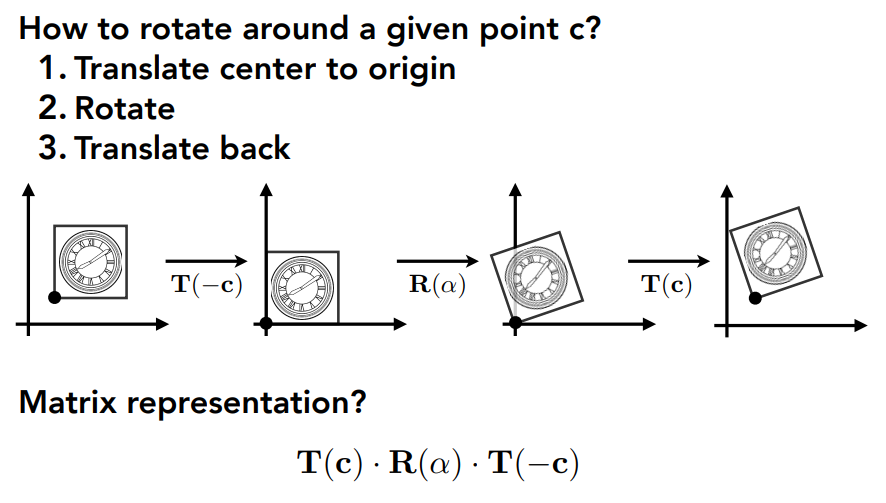
上例中我們要將圖形以其左下角的頂點 $c$ 做旋轉，而由於旋轉是以原點為基準在轉的，因此我們可以先將整個圖形平移回原點，轉完後再將其位移回去

三維空間的齊次座標

三維空間下的狀況也類似，多加上一個維度：

• 3D 點 = $(x,y,z,1{)}^T$
• 3D 向量 = $(x,y,z,0{)}^T$

同樣地，$(x,y,z,w{)}^T$ 代表三維空間中的點 $(\frac{x}{w},\frac{y}{w},\frac{z}{w})$，注意 $w$ 不為 $0$

伸縮

$$S(s_x,s_y,s_z)=\left[\begin{array}{cccc}{s}_x& 0& 0& 0\\ 0& s_y& 0& 0\\ 0& 0& s_z& 0\\ 0& 0& 0& 1\end{array}\right]$$

平移

$$T(t_x,t_y,t_z)=\left[\begin{array}{cccc}1& 0& 0& t_x\\ 0& 1& 0& t_y\\ 0& 0& 1& t_z\\ 0& 0& 0& 1\end{array}\right]$$

仿射

仿射轉換的矩陣寫法也類似：

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ z^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{cccc}a& b& c& t_x\\ d& e& f& t_y\\ g& h& i& t_z\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]$$

旋轉

$$R_x(\alpha )=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& cos(\alpha )& -sin(\alpha )& 0\\ 0& sin(\alpha )& cos(\alpha )& 0\\ 0& 0& 0& 1\end{array}\right]$$$$R_y(\alpha )=\left[\begin{array}{cccc}cos(\alpha )& 0& sin(\alpha )& 0\\ 0& 1& 0& 0\\ -sin(\alpha )& 0& cos(\alpha )& 0\\ 0& 0& 0& 1\end{array}\right]$$$$R_z(\alpha )=\left[\begin{array}{cccc}cos(\alpha )& -sin(\alpha )& 0& 0\\ sin(\alpha )& cos(\alpha )& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$

其中 $R_y$ 長得比較不一樣要注意一下